1.検定と推定
統計学はデータを数量化して母集団の特徴や傾向を分析したり、母集団からサンプルを抜き取り、この中から母集団の特徴を推測する科学的な学問です。
統計学は大きく記述統計学(descriptive statistics)と推測統計学(inferential statistics)に分けられ、前者は大量の数量データから母集団の性質を記述します。 集団の大きさや、平均値、標準偏差の統計量を読み取り性質を把握するもので、統計学の歴史的に最も早く発達しました。
一方の推測統計学は、母集団から抜き取った標本を使って母集団そのものの特徴を推測します。一般的なデータ分析では、限られた標本数しか得られないケースが多いため、一般的に統計分析を行う場合はこの推測統計学が用いられます。
有意差検定と区間推定は、後者の推測統計学の中核を成す手法です。統計的有意差検定とは、一定の確率の元で◯×判定を行うもので、言わば定性分析評価です。一方の推定は◯×の度合いがどの程度なのかを量的範囲で推定するもので言わば定量分析評価になります。
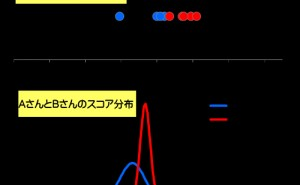
2.統計的有意差検定とは
有意差検定は◯×判定と述べましたが、詳細には一定の確率の元での◯×を判定します。例えばAさんとBさんどちらがボーリングがうまいのか、白黒をはっきりさせたい場合はどうすれば良いでしょうか?
何十ゲーム投げてもBさんがAさんの全ゲームのスコアをすべて上回っていれば、間違いなくBさんが強いと断言できます。しかし実際はスコアはばらつきますし、そこまで圧倒的な実力差が無い場合は容易に判断出来ません。そこで統計的に白黒を判定する基準を設定します。
ボーリングスコア
Aさん Bさん
1 130 149
2 109 152
3 134 144
4 149 137
5 132 145
平均 130.8 145.4
標準偏差 14.3 5.7
例えば上記のように5ゲームで勝負して、そのアベレージが高い方を勝ちとします。この5ゲームマッチを90%の率で勝て...
ただし判断の為に5ゲームマッチを10回も繰り返すのは現実的ではありません。そこで最初の5ゲームのデータから信頼率90%で判定を行うのが統計的有意差検定なのです。