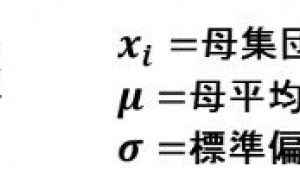【目次】
▼さらに深く学ぶなら！
「工程能力指数」に関するセミナーはこちら！
1．行程能力の指数化
前回のその1に続いて解説します。スペックに対し特性の分布がどの程度余裕を持って納まっているかを知る為の指標が、工程能力指数です。特性値の中心を決めるのが平均値とすれば、分布の範囲を決めるのが、バラツキといえます。 この場合バラツキは標準偏差σを基準として算出されます。
平均値と標準偏差を用いて工程能力を分かりやすく指数化したものが”工程能力指数”です。 一般的にCpの記号で表記されますがこれは、Process Capabilityの頭文字を取ったものです。
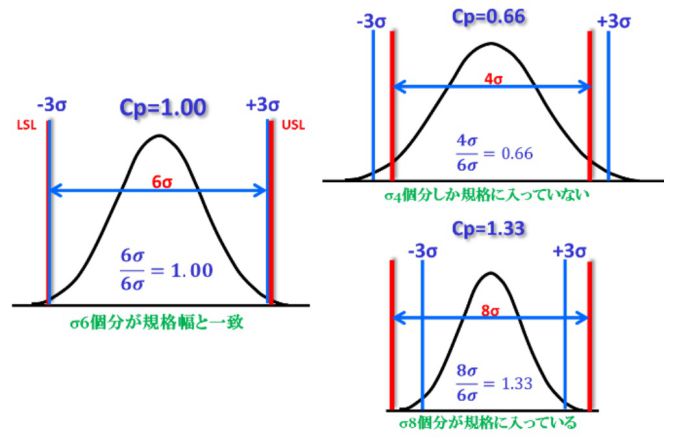
Cpとは工程能力指数で、特性値が規格範囲に収まっているかを観る指数です。例えば、部品の長さ規格が100±1mmだとすると、実際の製品の長さは99-101mmの範囲に100%収まっているのが理想です。然しながら同じ工場、同じ機械、同じ元材料、同じ作業者にて同じ様に加工したとしてもばらつきは発生します。
仮に100万個作ったら何個が規格外れになるでしょうか、それを知るための目安指標がCpやCpkと呼ばれる指標です。ばらつきを表す統計指標の1つに標準偏差σがあります。Cpは、その計算式から規格範囲内にσ何個分が含まれるか表していると言えます。
Cp(もしくはCpk)＝1.0の時は、造った部品の99.73%が規格内に収まり、約0.3%が規格範囲外となります。即ち100万個作成したら、2700個程度が規格から外れます。
一般にCp・Cpkの値は1.33以上は必要で、1.66以上が好ましいと言われます。1.33は0.006%が規格外になり、100万個のうち63個が規格外となります。 同様に1.66であれば0.00006%であり、100万個作成してわずか0.6個となります。
Cpは上...
大阪・日科技連 大阪事務所
