13.MTシステムで認識・予測する
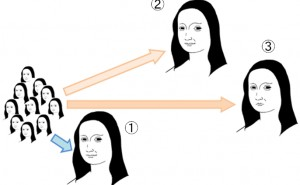
いくつかのモナリザの集団が左にあります。このモナリザには、起きがけや少し疲れたモナリザも含まれていますが、全て微笑みをたたえた本物です。
これに対して、3人の「私はモナリザよ」と主張する女性が居ます。 ①の女性は左の集団に近く、本物と判断されます。 しかし、②は目の間隔が広く、③は微笑んでいないために集団からの距離が遠く、本物とは判断されません。
14.モナリザの近さを測ると
このモナリザ達の表情は気分や時間によって少しばらつきがありますので、それぞれは必ずしもゼロ位置にはありません。1とか1.5という距離に居ることもあります。
ただ、それらの平均値は1になります。ですから、距離が2とか3になると「本物かどうか怪しい」ことになります。距離が10なら本人である可能性はゼロに近くなります。
15.パターンの距離
パターンの近さ、遠さをどのように求めるのかが問題です。パターンに1cm、2cmと同じように精度の良い目盛をつけるのです。 相対関係に注目した距離の計算方法があります。インドの数学者M博士が考案した方法です。相対関係だけではなく、目や口の大きさ、つまり構成要素の大きさも一緒に考慮します。
その計算方法とロシアの文豪トルストイの「アンナ・カレーニナ」とを結び付けて、パターン認識ができると考えたのが、T先生です。
16.アンナ・カレーニナとゼロ点
「アンナ・カレーニナ」の書き出しは次の通りです。「幸福な家庭は一様に幸福だが、不幸な家庭はそれぞれに不幸である」。
意味深い一節ですが、「一様」にポイントがあります。家族全員が健康で平穏無事…幸福な家庭とは、当たり前のものが揃っている一様なものだということです。その一様なところが原点すなわちゼロ点です。
それに対して、不幸な家庭は「それぞれの理由」を抱えていて一様ではない、ということです。
これには異論もあるでしょう。宝くじに当たる幸福もあれば、試験に合格する幸福もあるではないか、ということです。
しかし、宝くじに当たったとしても、後になれば「それは本当の幸福とは関係がなかった」と思えるのではないでしょうか。 ある方が、奥様が病気になられた時に「“無事”、つまり当たり前の日常の大切さを感じます」と漏らされました。幸福な家庭では、芯のところは皆重なっていて一様であり、それが“無事”という言葉に凝縮されているのだと思います。
17.幸福な家庭にある相対関係
幸福な家庭に共通する性質を見出すことができれば、幸福に関する距離を測ることができるはずです。家庭を構成する要素は一つではなく、たくさんあります。健康、仕事、希望…。家庭ごとにそれら構成要素の値や相対関係は少しずつ異なっています。健康な人でも、個人ごとに体温や血圧が少しずつ異なるように。
ただ、幸福な家族にある構成要素間の相対関係を調べると、規則性も見えてくるでしょう。その規則性か...
18.幸福な家庭の平均距離は1
アンナ・カレーニナをヒントに、M博士の数理を適用してパターンの距離を測ると「幸福な家庭の距離平均は1になる」のです。
この場合の距離とは原点からの距離です。たとえば幸福な100の家庭を集めて、家庭を構成するいくつかの要素に点数を付けたとします。それを集計してM博士の数理からそれが導かれるのです。家庭の幸福度距離を測るための単位量1が定義できたことになります。ちなみに、全ての要素の平均値を持つ家庭は距離がゼロです。
一様な状態を基準としてパターン距離を定義する数理、それはM博士の「相対関係を考慮した数理」である…T先生が20年ほどをかけてたどり着いた着想です。