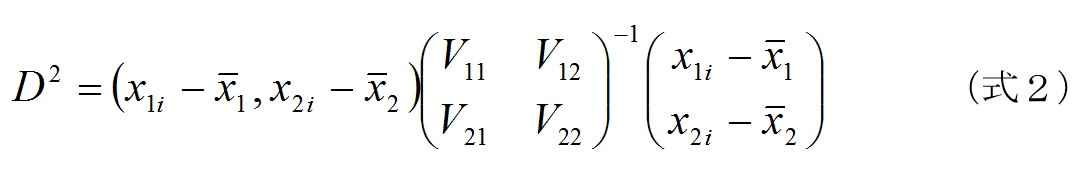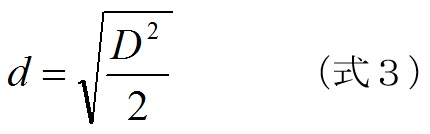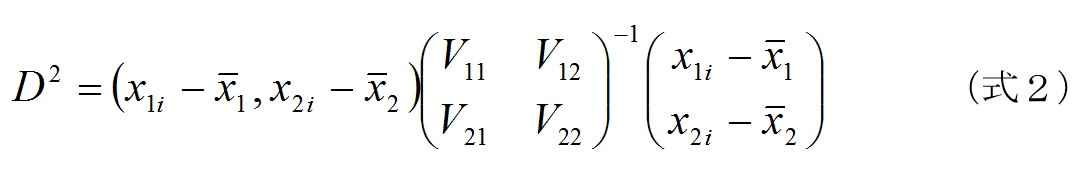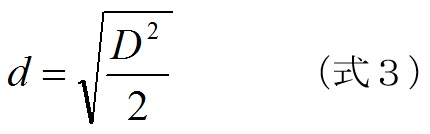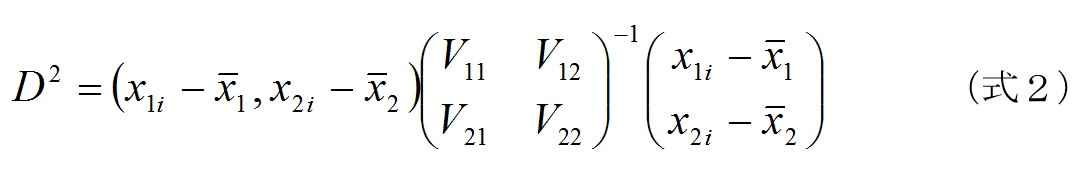タグチメソッドのMT法で一気に有名になったマハラノビス距離ですが、判別分析という昔ながらの統計的手法にも使われています。又、難しい式だと思われそうですが、なじみのふかいところでは、偏差値があります。偏差値というのは、下記のように計算されています。
実は、
の項が、一次のマハラノビス距離に該当します。10倍したり 50を足したりするのは、満点が100点の感覚に近づけるためであって、比較のためなら別になくてもよいのです。偏差値はその式が示すように、平均からの距離が遠いほど高くなりますが、ばらつきが大きければたいしたことないということで、ばらつきの尺度である標準偏差でわり、平均からの距離が何σ（シグマ）離れているかという、一種の標準化です。
の項が、一次のマハラノビス距離に該当します。10倍したり 50を足したりするのは、満点が100点の感覚に近づけるためであって、比較のためなら別になくてもよいのです。偏差値はその式が示すように、平均からの距離が遠いほど高くなりますが、ばらつきが大きければたいしたことないということで、ばらつきの尺度である標準偏差でわり、平均からの距離が何σ（シグマ）離れているかという、一種の標準化です。 数学の点数が90点だといっても、平均が90点なら、偏差値50で、平均が50点で標準偏差が2点なら70にもなります。前者は簡単な問題だったので、だれでも高得点だったこと示しますが、後者は、問題がむずかしく、ほとんどの人が50点前後のところを90点もとったのですから、かなり数学の成績が良いということになります。このように相対的な比較をするには非常に便利な式です。
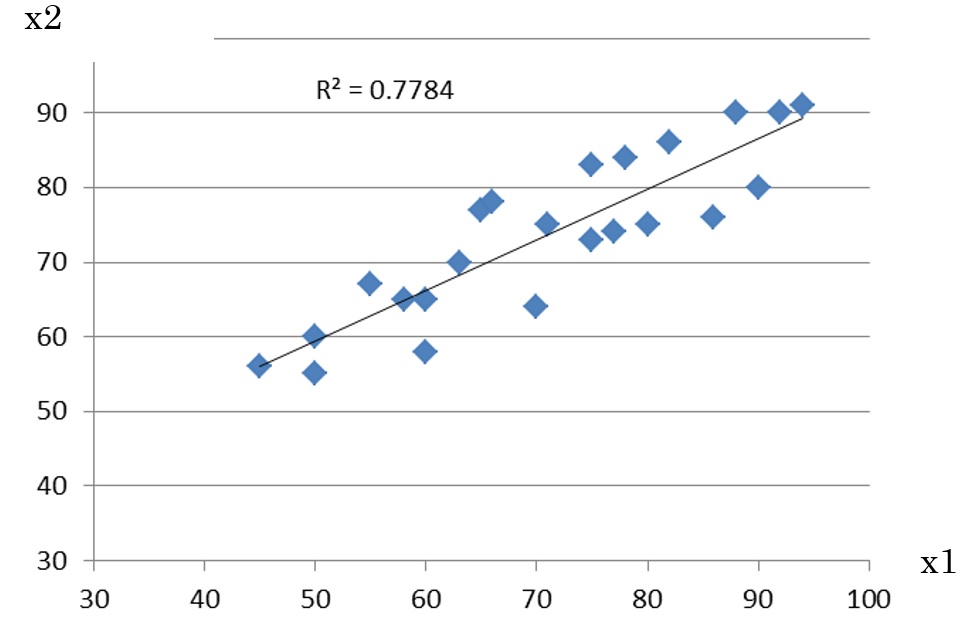
こんどは、項目が二つあるような場合を考えましょう。数学と理科の試験点数でもいいのですが、話の焦点に近づけていきたいため、ある電気製品の工程内検査項目にします。ひとつは、電流特性（x1）とし、もうひとつは電圧特性（ⅹ2）とします。また、これらに相関関係がある場合です。数学の出来と理科の出来がゆるやかな正相関のようなものです。あるときの製品工程検査データを座標プロットすると、図1のようになったとします。
図1．工程内検査値のプロット
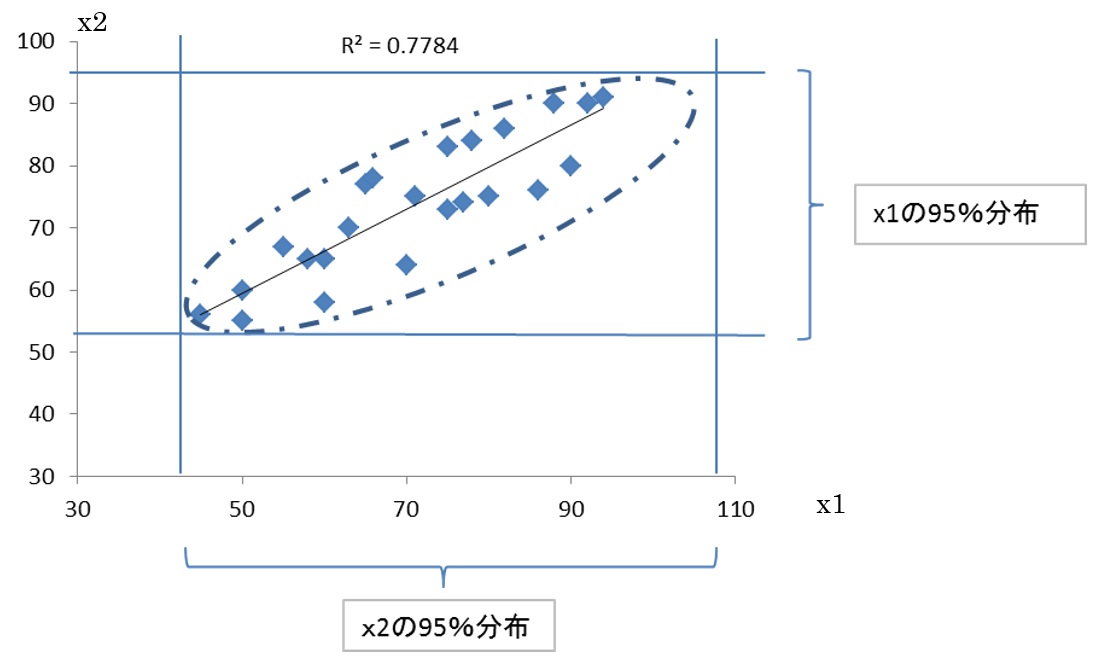
ここで、だいたいの分布に線をひくと下図のように楕円形になります。（ここでは感覚的な理解でかまいません） 次に、x1、x2の管理限界線を引きます。これも大体でいいでしょう。通常平均値±2σや3σ、95%信頼限界とかで管理します。これらを図示したものが、図2です。
図2 管理限界線として引いた分布線と相関データの周辺を囲んだ図
図2では、95%信頼区間を引いていますが、3σ管理ならここが平均値±3σに変わるだけです。そこで、図3をご覧ください。★や●データを異常判定できるかどうかです。
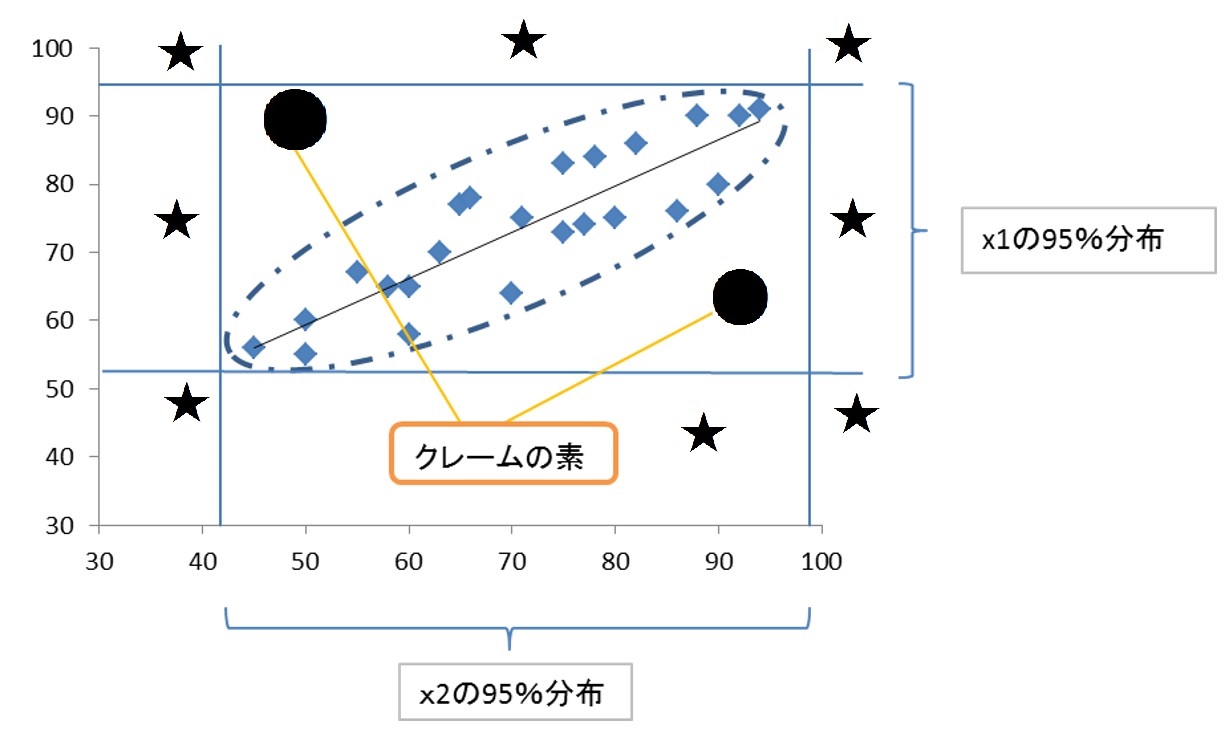
図3 管理限界線と異常データ
★印は、一個一個の項目の管理をしていれば、つかまりますから、こういう管理（3σ管理の親戚）は有効です。ところが、● 印は、楕円からずれているので、二次元の分布からは外れている点で異常ですが、一軸方向からみているかぎり、管理限界線内のため、つかまりません。通過してしまいます。これが、クレームの素になったりします。
この場合の管理限界線は、直線で縦横にひいたものでなく、楕円だということです。（実際、これは楕円になることが数理的に証明されます。）この楕円の方程式をだすときに、マハラノビス距離が必要になってきます。マハラノビス距離による管理限界線でなければ、クレームの素が生まれます。
不良が工程内検査で簡単につかまるなら、クレームになりません。流出するからクレームになるのです。（信頼性の問題は別）この点からすれば、図3の● データは通常の管理ではつかまりませんから、流出してしまいます。
この例は、実は、半導体の実例としておこったことです。半導体では、電流特性として電流増幅率が、電圧特性として1次降伏電圧があります。降伏電圧の逆数は電流増幅率に比例するので、図1のような相関があるのです。しかし、● 印データが発生することがあります。「異品種混入」です。パターン面積や形状が違う異品種が混入すると、図3のような事態が起こります。通常の3σ管理や95%信頼区間管理ではつかまりません。よって、相関を含めた管理＝マハラノビス距離が重要になります。二項目の場合のマハラノビス距離は、以下のように計算されます。
（通常はこれを項目数2でわり平方根をとりますが、式2を単にマハラノビス距離という場合もあり注意が必要です。）Vは分散ならびに共分散です。この定義は統計の本をご覧ください。式2を項目数の2でわり平方根をとったあとのマハラノビス距離をdとすれば、
この距離が、95%信頼区間にはいるには、棄却限界値から、
です。
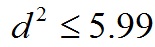
です。 5.99という数値は2変量の場合の外側に出る確率が5%（信頼水準が95%）の場合の限界棄却値です...
からきています。これを式2にいれると、楕円の方程式となります。計算方法の説明は、ここでは詳しくしませんが、散布図からみれば、その概念がわかりやすいと思います。実際の工程検査は、もっと多くの検査項目や管理項目があります。これでは、二次元グラフ（散布図）を書いていては追従できません。3次元以上は、マハラノビス距離でなければ何ともならないということです。（二次元ぐらいであれば、散布図をいちいち書くという手段もありますが）
