Ω（オメガ）変換とは　　　

1. Ω（オメガ）変換が必要な理由

　歩留り90%のものを95%にするのは、歩留り30%を60%にするより難しいといいます。これは元々よいものをさらによくするのは、悪いものをよくするより難しいということです。本当でしょうか？　又、不良率が2%だったものが1%になったとします。これは、半減したといえるのか、1%だけ不良が減ったと考えるのか、どちらでしょうか？もし、半減したとしたら、大きな効果です。その対策を不良率100%のものに適用したら50%になるはずです。

　もし、1%の効果と考えれば、99％にしかなりません。歩留り30%のものを歩留り60%にできる対策ができたとして、同じ対策を歩留り80%に適用しますと、先ほどの効果を30%アップと考えれば、110%です。すでにおかしい話になっていますが、倍増効果で計算すれば、160 %となり、全くおかしい話になります。このように、歩留りや不良率でデータをとった場合、その効果の考え方次第で、改善策などの予想が困難になります。これは、一元配置実験のような基本的な実験から直交表を使った実験、あるいは回帰分析（重回帰分析含む）等々での効果算定（予想、推定あるいは判断）に不都合をもたらします。

2. なぜ、効果算定で変なことが起こるのか？

　我々は、効果の算定を単純な差分や割り算で考えます。このとき、まずは、数値がマイナス無限大からプラス無限大まで存在できる対象物であれば、上記のような計算上の矛盾はとりあえず生じません。歩留りや不良率は0から100%の間でしか存在しないので、こうしたことが起こります。そこで、0から100%（小数でいえば、0から1）の世界をマイナス無限大からプラス無限大の世界へ変換することが必要となります。かつ、効果の差分が効果であるように変換しておけば簡単なわけです。（難しい言葉で、加法性を上げる、とかいいます。足し算モデルへの変換です。）

　歩留り問題だけだと思ったら、大間違いです。数値範囲が有限であれば必ず同様のことがおこります。

　たとえば、ある面積Sの基板内の温度分布を評価する際、温度Tの分布面積をｘとすれば、このｘは0≦x≦S　ですから、両辺をSでわれば、0≦x/S≦1　となり、歩留り問題と同じことになります。又、以下のようにも拡張することができます。むしろ、しなければいけません。

　　　　　　　L≦x≦U 　　  　　 　 eq1　であれば、

                    L-L≦x-L≦U-L          eq2

                    0≦(x-L)/(U-L)≦1    eq3

                   ここで、 p=(x-L)/(U-L) とおけば、歩留り問題と同じになります。

　そこで、つぎにどう処理すればよいのかを結論から説明します。理由は後回しです。

3. そこででてきた“オメガ変換”　（Ω変換）という変換式

　どうしてそうなるのかはさしおいて、とりあえずオメガ変換というものを使いましょう。この式は、非常に簡単です。この式で変換すれば、その効果は差分で考えてよいということになります。これは、単純な歩留り比較のみならず、実験計画法における分散分析でも非常に重要な（難しく言うと加法性の確保）変換です。その式は、ｐを０から１の小数とすれば（0%から100%）、以下のようになります。

　　　　　y=10 ＊ LOG(p/(1-p))   eq4  　(db:デシベル)

  上式をオメガ変換といいます。単位は無名数で、一応、デシベル（db）といっています。＊は掛けるという意味です。わざわざ書いたのは、エクセルでよく、＊をつけわすれるため、注意しなさいということです。LOGの底は10で、常用対数です。

　よく似た式でロジット変換というのがあります。同じ働きをもっていますが、対数の底が、e：超越数ですから、自然対数となります。数学屋さんはこちらを使います。又、10倍しません。一応、数式を書くと、

　　　      y=ln(p/(1-p))　      eq5 　ロジット変換(デシベルとかつけない。)

　たいていのエンジニアは　eq4のオメガ変換を用います。数理的にはロジット変換の方が美しいのですが、会議なんかで議論、発表するとき、ロジット変換では、「効果が5です」、みたいな言い方になってしまいます。語尾が弱い。オメガ変換なら、「5デシベルの改善です」、とかいえるので、変な語尾になりません。会話がしやすいのです。これが、エンジニアが使うメリットでしょうか。本当のところはしりません。統一さえすれば、数理上はどちらをつかってもいいのです。

4. 事例で確認しましょう

　1項の「歩留り90%のものを95%にするのは、歩留り30%を60%にするより難しい」という話が本当かどうか、オメガ変換によって確認しましょう。

　90%のオメガ変換をy1とすれば,

　　y₁=10×LOG(0.9/0.1)=9.5424 db　  　　eq6　　

  95%のオメガ変換をy2とすれば、

     y₂=10×LOG(0.95/0.05)=12.7875 db     eq7

  30%のオメガ変換をy3とすれば、

      y₃=10×LOG(0.3/0.7)=-3.6798 db        eq8

  60%のオメガ変換をy4とすれば、

　   y₄=10×LOG(0.6/0.4)=1.7609  db         eq9

  90%を95%にする改善効果は、eq7とeq6の差分で決まります。これを∆₁₂とします。

  　 ∆₁₂=12.7875-9.5424=3.2451 db　    　eq10

  30%を60%にする改善効果は、eq9とeq8の差分で決まります。これを∆₃₄とします。

　  ∆₃₄=1.7609-(-3.6798)=5.4407 db        eq11

   となります。すなわち、30%を60%にする効果の方が高いので、世間で言われていることはウソだということになります。

　しかし、もしも90%を95%でなく97%に改善したとしたら、そのオメガ変換の差分は5.5541 db.となり、30%を60%にする効果より大きいということになります。裏返せば、90%を97%にするのは30%を60%にするより難しい、といえば正解だということです。

　計算すればわかってきますが、歩留りが90%以上（不良率が10%以下）の場合や、歩留りが10%以下（不良率が90%以上）のような場合は、ちょっとしたパーセント変化でオメガ変換効果の値が大きく変わります。よって、10%以下とか、90％以上の場合の比較には、オメガ変換はとくに必須の手法だということになります。先ほどの例でも、95%を97%に変えただけで結論が変わってきたことに注意してください。（変わってよいのです）

　1項に示した他の事例でもオメガ変換を行い、どういう結論になるのか計算してみてください。なお、オメガ変換の分数部分ですが、品質工学などでは通常は分子に良さ加減を、分母に悪さ加減をもってきます。以下に述べるSN比（よさ加減）から考えるからです。上に悪さ加減をもってきたときには、正負が逆転します。当たり前ですが、注意が必要です。

　なお、次項は興味がなければ、読まなくても構いません。理解できない公式でも、認められた公式であれば、どんどん使っていいのです。いちいち数理の基礎を理解しないと使えないわけではありません。正規分布の正確な式を知らなくても、正規分布近似で物事をすすめている人はいっぱいいることと同じようなものです。

5. オメガ変換の数理的な説明

　統計的には非常に難しい説明がなされているので、ここではしません。オッズ比とか、そういう類の統計学をご存知の方は、オッズ比の対数であるということでおしまいです。しかし、オッズ比自体、これを理解するのは結構難しく、統計初心者には無理です。又、私自身、これで説明したことはありません。以下に、簡単な説明をしてみます。おおやけに認められている説明ではありませんが、「わかった気になるには」これで十分です。前項にも述べたように、わかった気になって安心しているだけで、本当はわかっていないという場合、実害がある場合もありますが、この場合は公式頼みで実害ありません。（たとえば、標準偏差の意味を正確に知ってなくても、何とか使いこなしています。大きな実害はありません。逆に、管理図の3シグマ法なんかは、単純な3シグマの計算法では、管理限界線の計算を間違えてしまいます。公式通りでいいのです。）

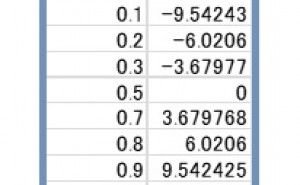
　数理の説明の前段階として、まず、オメガ変換を簡単に図示してみましょう。横軸をｐとして、縦軸をそのオメガ変換値ｙとしたグラフは下記、表1, 図1のようになります。 　　　　　　　　　　　　　　　　　　　　　　

　表１

図1　　　　　　　　　　　　　　　　　　

　図１では、pがゼロ付近で、ｙ（オメガ変換値）はマイナス無限大へ、ｐが1付近でプラス無限大へ向かっていることがわかります。歩留り50%（p=0.5）でｙはゼロです。歩留りが半分の地点をゼロにしているわけです。なにはともあれ、0から１の間の数値が変換によって－∞から＋∞になったので、2項の前半に述べたような「矛盾」はまず起こらないということがわかると思います。これは基本的な確認ですが、重要なことです。又、グラフからｐが０や１付近では急激な変化がｙに起こっています。いいかえると、この付近での加法性は％データでは無理だということです。4項の95%と97%の違いを思い出してください。

　数理上の簡単な説明にうつりましょう。

 (1) y=10LOG(p/(1-p)) =10LOG(p)-10LOG(1-p)  eq12 と、考える。        

   上式は、=10LOG(良品率)-10LOG(不良率)　eq13 を表現しています。

　つまり、歩留り（良品率）をpとすれば、不良率は1-pですから、オメガ変換というのは良品率と不良率の違いを足し算モデル（差分）に置き換えているということです。良品率と不良率の違いが足し算モデルとして説明されるわけですから、良品率や不良率が変わったときにも足し算モデルとして計算するので、足し算モデルが保存されるということになります。よって、オメガ変換すれば効果の大きさに足し算モデルが成立することになり、上記のような効果計算が成立するという考え方です。このいい加減な説明では納得いかない場合、次の品質工学的な説明が次に簡単な証明です。

 (2)品質工学で使われる望目特性SN比からの説明

　この説明方法の欠点は、品質工学のSN比に関する知見がない人には、却って難しいということです。品質工学の基本的な計算である「望目特性のSN比」の算出に慣れていらっしゃる方にはわかり易いと思われます。ここでは、わかっている人向けに解説します。わからない人は品質工学の基本書を読んでください。

 （説明）

　不良に0、良品に1という特性値をとったとします。100個中、5個が不良なら、そのデータは、0が5個、1が95個並んでいることになります。これを（0，1）法ともいいます。

　良品率ｐは、p=(y_1+y_(2+)⋯+y_n)/n　      eq13

　全変動は、  S_t=y_1^2+y_2^2+⋯+y_n^2   eq14　　 

  平均変動は、S_m=(y_1+y_2+⋯y_n )^2/n     eq15 は、0又は1ですから、eq15は、

                   S_m=(y_1+y_2+⋯y_n )^2/n=(np)^2/n=np^2    eq16　

  誤差変動は、S_e=S_t-S_m=y_1^2+y_2^2+⋯+y_n^2-(y_1+y_2+⋯y_n )^2/n     eq17 ですが、 y_(1  ),y_2,⋯,y_n  は、0又は1ですから、二乗しても0か1で変わりません。よって、  eq17は以下のように書けます。

　　　　　　S_e=y_1+y_2+⋯+y_n-np^2    eq18
                       =np-np^2                             eq19
                        =np(1-p)                              eq20　　

6. オメガ変換値での効果有無判断

　オメガ変換は、一言で言えば「壁のある数値の壁を取っ払い、効果の加法性を確保した変換である」ことが第一義で、本来は有意差検定などと違い、何デシベルの差があれば有意であるとか、効果があるとかは関係ないのです。ただ、品質工学では一応、3db以上の差をもって効果ありとか、違い有りとかいっています。3db向上というのは、σの二乗が半減したということになります。（σ換算では0.7掛け）

　これは、有意差検定とどういう関係があるでしょうか？　本来は関係ありません。オメガ変換というのは、効果の加法性を確保するためのモノであって、有意差検定とは関係ないのです。しかし、3dbの差があるというのと9dbの差があるのとでは、あきらかに後者の方が高度に有意に思えます。この観点から3dbというのは、はたして何％ぐらいの有意水準に該当するのでしょうか？

　通常、標準偏差の有意差検定は、F検定で行います。

    F=(σ_1^{^}2)/(σ_2^{^}2 )       (σ_1>σ_2 )                    eq24

サンプルサイズを変えながら、ただし簡単のため、1と2は同サイズとして、F値は以下のようになります。eq24が下表F値より大きくなれば有意として判定されます。　　　　

　表2

図2

　表2や図1から、サンプルサイズが25個を超えると、有意水準5％では1.98ほぼ2 がF値になっています。（σの二乗が半減に該当）　このことから3db有効説というのは、有意差検定からも妥当な見方であることがわかります。逆に、サンプルサイズが小さくて20個以下の場合には、有意水準5%では（3dbの差があっても）有意とは言えません。ただし、この場合でも加法性は成立しています。そちらの方が重要...