今回は、母集団が正規分布であり、平均値と分散値が既知である場合の検定事例を取り上げます。
小学校4年生のある年の全国身長調査で平均値は143.5cm、分散は7.8×7.8cm2でした。5年後に小学4年生の中から無作為に100名を選び出して調査した所、標本の平均値は144.9cmでした。 この5年間で平均身長は変化したと言えるでしょうか?
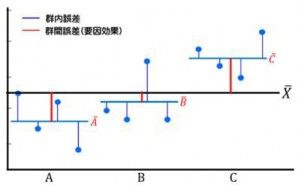
変化したかどうかの検定なので5年前の平均値より小さい場合と大きい場合の両方を検定します。このように下側と上側両方の検定を両側検定と言います。 一方で、大きくなかったか(もしくは小さくなったか)どうか片側だけを検定する場合は片側検定です。
両側検定での帰無仮説と対立仮説は以下のようになります。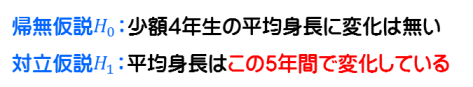
この場合は、まず標本平均の分布を考えます。100個のサンプルデータの平均は、当然ですが変動することで分布が生じます。確率変数Xが正規分布に従う場合は、その平均値も正規分布となります。 よって標本の平均分布も正規分布形状となり、その分布の中で滅多に見られない両端側の値が出るかどうかで有意差を判定します。
標本平均の平均値は母集団平均値と同じく143.5cmですが、分散値は母集団の分散をサンプル数で割った値(=7.8×7.8/100)です。 平均値の分布なので、個別データの分布よりもばらつきは小さくなります。有意水準5%で両側検定した時のグラフは下のようになります。
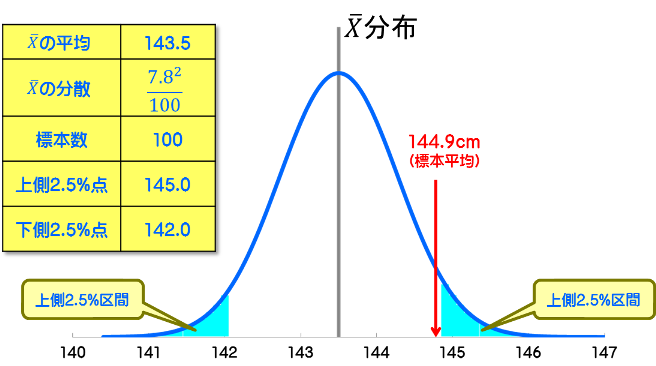
グラフで水色で示している有意水準領域を棄却域と呼びます。平均値の分布で上側2.5%に相当する点は145.0cmとなり、検定統計量は144.9cmとわずかに小さく棄却域には入らないため、H1は支持されずに、帰無仮説H0は棄却出来ない、つまり4年生の身長は「5年で変化しているとは言えない」という判定になります。
あらためて注意しておくと、棄却域に入らずH1が支持されなくても、H0が積極的に採用されるわけではありませんから、身長が変化していないと断言することは出来ません。あくまでも「変化しているとは言えない」という判定となります。
では次に、5年間で身長は大きくなったのかどうかを、有意水準5%で上側検定してみます。帰無仮説と対立仮説及び母平均分布を、下の図に示します。
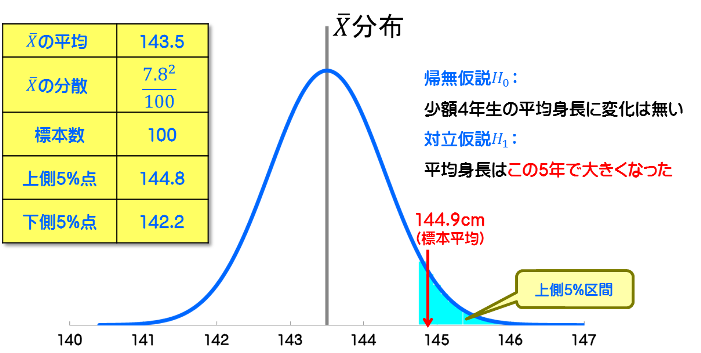
片側検定の場合は有意水準の確率はそのまま適用され、上側5%点は144.8cmなので棄却域はそれ以上の領域となります。検定統計量144.9cmはこの棄却域に含まれますから、対立仮説H1が採用され帰無仮説H0は棄却されます。 つまり...