今回は、次の事例をもとに、検定推定を行う手順を解説します。
1. 二つの母分散の比に関する検定と推定
事例として、ゴルフシャフトの補強用で超強度の特殊糸を製造している向上での課題からです。今回、新規設備投資を行い、特殊糸の更なる強度向上を行いました。
データAは、従来設備から製品をランダムに10回抜き取り、強度測定したデータです。
データBは、新規設備から製品をランダムに８回抜き取り、強度測定したデータです。
データBは、新規設備から製品をランダムに８回抜き取り、強度測定したデータです。
設備更新後、特殊糸の強度のばらつきはどうなのか、又、強度の平均値は向上したのか、二つの母分散の比に関する検定と推定を行う手順を考えましょう。
A: 96,105,101,99,103,97,100,101,95,103
B: 98,110,108,106,107,104,99,108
B: 98,110,108,106,107,104,99,108
検定推定の目的は、ある仮説が正しいかどうかを統計的に判定するものです。統計ですから間違っている可能性がありますので、その判定基準を予め決めておき（一般的にはP値：5%）客観的に判断する方法です。統計的仮説検定を活用することにより、無駄なサンプル収集を防止でき、結論を先延ばしせずに効率よく最終判定に辿り着くことができます。以下の計算結果はMinitabのソフトを使用しました。他の統計ソフトでも同じ答えになります。
2. 仮説（検定の目的）を明確にします
① 設備更新（新規）により当初想定（例：5.0の向上）とおりに平均強度が増加しているか、少なくとも平均値が3.0以上向上しているか確認したい
⇒想定とおりの強度向上が見られない場合は設備改造が必要です。
② 設備更新（新規）の目的が旧機との入れ替え又は増産であれば、平均強度が旧機と同等かどうかを確認したい。（例：平均値の差が＜2.0であれば同等と見なす）
⇒同等でなければ設備改造が必要です。
③ 設備更新（新規）で強度低下が無ければ良い。
⇒少しでも強度が向上していれば更新設備を使用したい。
3. 今回のサンプル（18個のデータ）から分かることを確認する
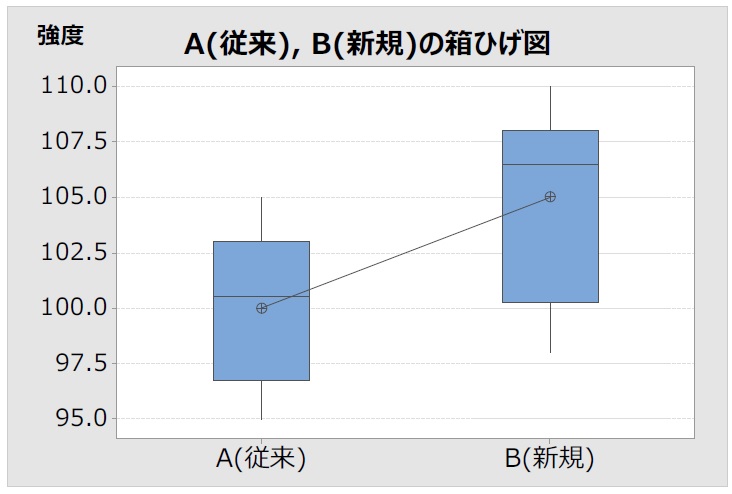
《手順1》データの視覚化 ⇒箱ひげ図がお勧めです。
・従来と新規のばらつきに差は無さそうだ。
・新規の平均値が5程度向上している
・新規の平均値が5程度向上している
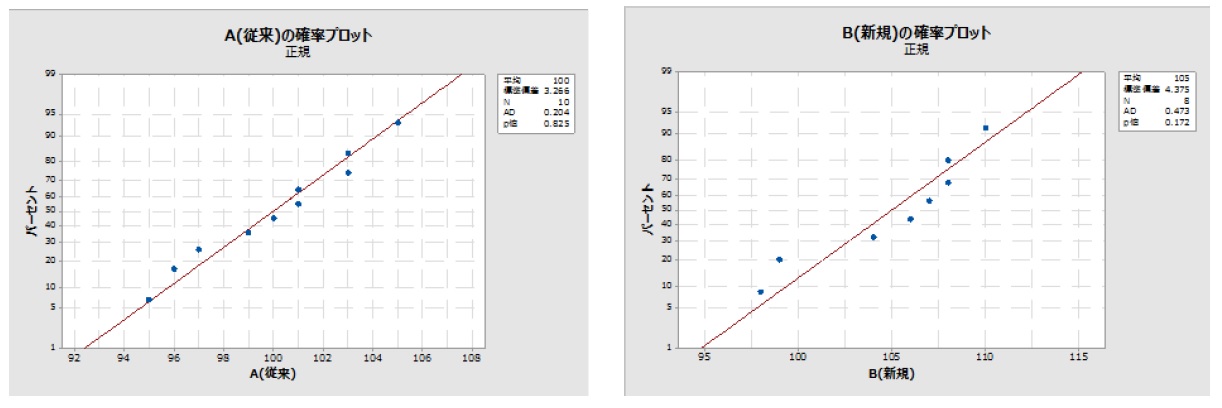
《手順2》データに異常がないか確認する ⇒正規性検定がお勧めです。
・従来：P値：0.825、新規：P値：0.172
何れも＞0.05 でありデータに異常は無いと見なします。
何れも＞0.05 でありデータに異常は無いと見なします。
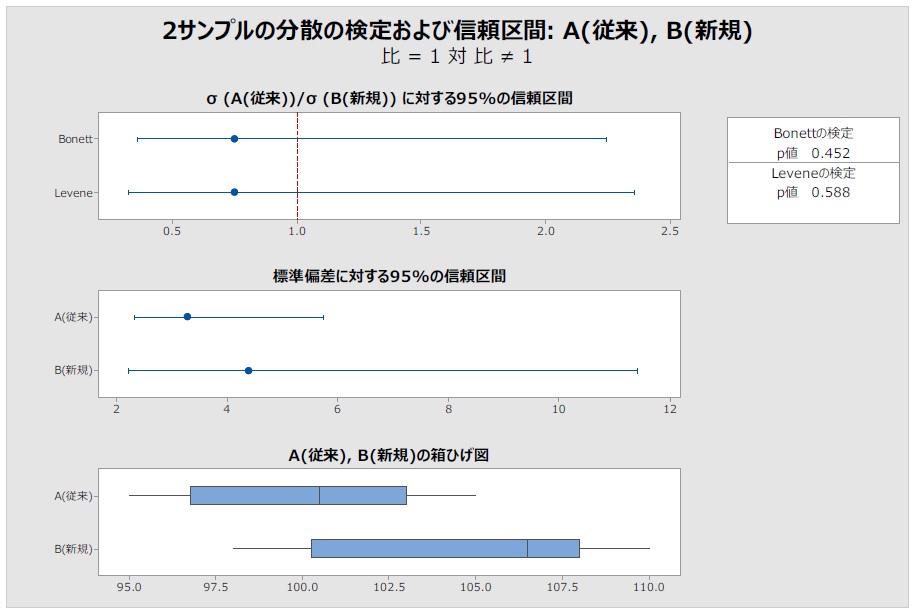
《手順3》等分散性を確認する
この目的は、ばらつきの変化を検定するのではなく、平均値の差の検定の前提条件（２つのデータが等分散であること）の確認です。 ⇒バートレット検定がお勧めです。
・P値：0.452＞0.05 ですので等分散とみなし、平均値の検定《手順４》に移ります。等分散でない場合は別の検定ツール（中央値の検定）を用います。
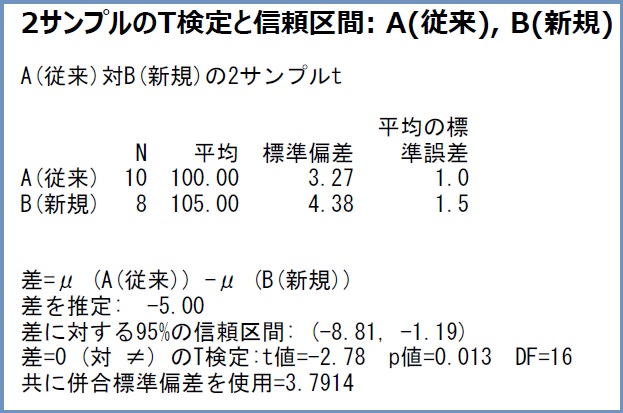
《手順4》平均値の差を検定する ⇒2サンプルｔ検定又は分散分析（一元配置）がお勧めです。
・P値：0.013＜0.05 ですので従来と新規では０を超える差があると判断できます。
・平均値の差の信頼区間：1.19～8.81
・平均値の差の信頼区間：1.19～8.81
4. この結果から分かること
仮説（目的）が①であれば、
・平均値の差は5.0であり、想定とおり向上しているが、平均値の信頼区間の下限が1.19であり、少なくとも3.0以上の条件は満たしていない。信頼区間を狭くするにはサンプル数を増やす必要があるので、
・検出力（0.9）、危険率（0.05）、今回のデータの標準偏差（3.8）を用いて、知りたい差（δ：3.0）を検定するために必要なサンプル数を求めます。
従来、新規 それぞれのサンプル数が35以上になるように追加データをとり、《手順１》～《手順４》で検定します。検定結果、
・信...
