トポロジーとは
トポロジー(topology)は、数学の一分野であり、空間の形状や物体の連続的な変形に焦点を当てています。その本質は「変形可能性」にあり、物体が伸ばされたり曲げられたりしても、その基本的な性質が変わらないことを扱います。例えば、ドーナツとコーヒーカップは、トポロジーの観点からは同じ物とみなされます。どちらも一つの穴を持つ形状であり、一方を他方に変形することが可能です。トポロジーは、物体がどのように連結されているか、穴がいくつあるかなど、「連続的な変形」によって変わらない特性を研究します。この分野は数学の基本的な概念を形成し、多くの他の分野への応用もあります。
トポロジーの応用
物理学
物理学におけるトポロジーの応用は、素粒子物理学や凝縮系物理学における基本的な概念として重要です。トポロジカルな概念は、素粒子の挙動や物質の相転移を理解するための鍵となります。例えば、量子ホール効果やトポロジカル絶縁体の研究では、トポロジーが中心的な役割を果たしています。これらの現象を理解することは、新しい物質の開発や量子コンピューティングの進展に直結し、物理学の未来を形作る重要な要素となっています。
コンピュータネットワーク
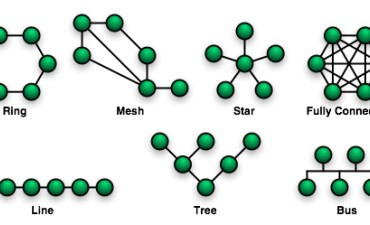
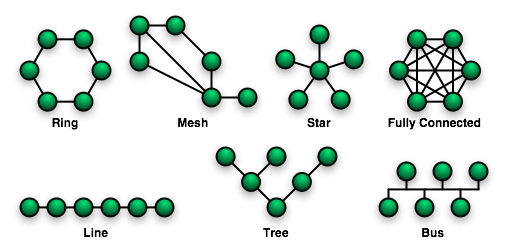
コンピュータネットワークにおいて、トポロジーはネットワーク構造の基本を形成します。ネットワークトポロジーは、デバイス間の物理的または論理的な接続方法を定義し、星型、バス型、リング型、メッシュ型など様々な形態を取ります。これらのトポロジーは、ネットワークの性能、耐障害性、拡張性に影響を与え、最適なネットワーク設計を決定する上で重要な役割を果たします。特に大規模なネットワークやクラウド環境においては、適切なトポロジーの選択がシステムの信頼性と効率を大きく左右します。
地理学
地理学におけるトポロジーの応用は、地図作成や地理情報システム(GIS)の根幹を成すものです。トポロジーは地図上の異なる要素間の空間的関係を表し、これは地図の正確性と有用性に直接関係します。例えば、GISでは道路、河川、土地利用などの地理的な要素がどのように相互作用し、接続しているかを解析するためにトポロジーが用いられます。この分野でのトポロジーの応用は、都市計画、環境管理、災害対策など、様々な実用的な応用に繋がっています。
トポロジカル絶縁体とは
トポロジカル絶縁体は、近年発見された物質のクラスで、その独特な電子構造が物理学界に革新をもたらしました。この物質は、内部が絶縁体である一方で、表面に特殊な金属的性質を示す電子状態を持っています。内部では電子が動かないため電流を運ぶことができませんが、表面では電子が自由に動き回り、電流を運ぶことができます。
トポロジカル絶縁体の表面状態の最も注目すべき特徴は、それがトポロジー的に保護されていることです。これは、表面上の電子が特定の方向にしか動けないということを意味し、これが外部の摂動や不純物の影響を受けにくい原因となっています。この性質は、物質が外部の変化に対して非常に安定していることを意味し、これが次世代の電子デバイスや量子コンピューターへの応用を可能にします。
トポロジカル絶縁体の研究は、物質のトポロジー的性質と量子力学の関係を深く掘り下げています。これらの物質は、量子ホール効果やスピントロニクスなど、新しい量子現象の理解に貢献しており、これらの現象を利用した新しい技術の開発が期待されていま...