◆ 充填率計算 面心立方格子
面心立方格子の充填率を計算します。格子定数を一辺の長さaの立方体とすると単位格子の体積Vaは式(1)となります。
Va=a3 (1)
また、原子の半径をrとしたときの原子一つの体積Vrは式(2)となります。
Vr=4πr3/3 (2)
そして、単位格子の中にある原子の数は各面に6個、単位格子の頂点に8個です。面にある原子は半分(1/2)単位格子に含まれます。頂点にある原子は単位格子に含まれるのは1/8個となります。それを踏まえて、単位格子に含まれる原子の数Nを計算すると式(3)となります。式(3)より格子定数の中には4個の原子が占めていることになります。
N=6(個)×1/2(割合)+8(個)×1/8(割合)=3+1=4(個) (3)
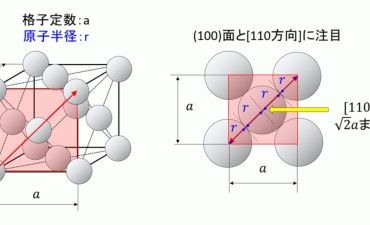
格子定数と原子半径の関係ですが、面心立方格子の(100)面および[110]方向に注目すると、下図より[110]方向の長さLは格子定数aで表すと三平方の定理より式(4)となります。また、[110]方向には原子がすき間なく3個並んでいます。3個の原子のうち両脇の原子は半分のみ(100)面に含まれます。そのためLを原子半径で表すと式(5)のようになります。式(4)、(5)より格子定数と原子半径の間には式(6)、(7)が成り立ちます。
L=√2a (4)
L=4r (5)
√2a=4r (6)
a=4r/√2 (7)
図.面心立方格子の格子定数と原子半径
式(1)~(3)を合わせると充填率Sに対して式(8)の関係式が成り立ちます。式(8)に式(7)を代入すると式(9)となり、計算すると式(10)、(11)になります。√2π/6を近似計算すると約0.74(74%)となります。これが面心立方格子の充填率です。また面心立方格子は最密充填構造です。最密充填構造の充填率は74%である、と表現することが出来ます。
次回に続きます。