1.相関分析とは
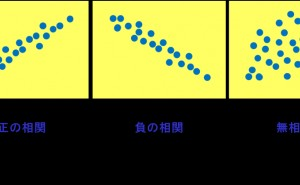
相関分析とは2つの変数の関係性を解析する分析法です。QC7つ道具の一つに図1の散布図があり、これは2つの変数に対応するデータを打点して相関の有無を見る手法ですが、相関分析は相関の有無や相関の強さを、統計的に算出した値から判断します。
図1 散布図
2.共分散とは
相関図を描けば正の相関、負の相関などと、変数同士の関係がイメージとして容易に掴めます。一方で相関の有無及び正の相関か負の相関かを数値で示してくれるのが共分散です。
二つの変数XとYの共分散を考えます。それぞれn個のデータがありx1はy1に、xnはynに対応しています。XとYの平均をXaとYaとし、各データと平均値の差が"偏差"となります。
| データ数 | X | Y | Xの偏差 | Yの偏差 |
| 1 | x1 | y1 | x1-Xa | y1-Ya |
| 2 | x2 | y2 | x2-Xa | y2-Ya |
| ・・・ | ・・・ | ・・・ | ・・・ | ・・・ |
| n | xn | yn | xn-Xa | yn-Ya |
偏差はデータの値が平均値より大きければ正の値、小さければ負の値を取るので、XとYとの偏差の積も正と負の両方の値をとります。XとYの平均値Gを中心として4つの領域に分けると偏差の積の符号は下の図2のようになります。
図2 平均値に対する偏差の積の符号
Gに対し右上と左下エリアは偏差の積の符号が正となる、つまり正の相関を示すデータはこの領域に多く、一方右下と左上エリアは偏差の積の符号が負となり、負の相関を示すデータが多くなります。従ってこの偏差の積の和をQxyとすると、Qxyの符号で正の相関か負の相関かが判断出来ます。
このQxyの値はデータが多ければ値が大きくなるので、Qxyをデータ数nで割って正規化した値Sxyを共分散とします。共分散は次式で求められます。
データ数が多くなるとこの式で計算するのは大変なので、エクセル等の表計算ソフトを用いる方が効率的です。またエクセルには共分散を計算する関数COVARがあり、2変数のデータを指定すれば簡単に値を求めることが可能です。
3.相関係数とは
共分散を求めることで正の相関か負の相関かは解りますが、相関の強さはわかりません。共分散の数値の大きさはデータの単位によっていくらでも変化し、相関の程度とは関係無いからです。
この様な共分散値の欠点を解消するのが"相関係数"です。相関係数は下の式で求められて-1~1の間の値を取り、数値が-1に近ければ負の相関が高く、1に近ければ生の相関が高くなります。
相関係数はエクセル関数CORRELを用いることで簡単に求めることが出来ます。上述の共分散値と同様に相関を見たい2変数のデータを指定して算出します。
4.相関係数の計算例
| No. | 身長 | 体重 |
| 1 | 147.9 | 41.7 |
| 2 | 163.5 | 60.2 |
| 3 | 159.8 | 47.0 |
| 4 | 155.1 | 53.2 |
| 5 | 163.3 | 48.3 |
| 6 | 158.7 | 55.2 |
| 7 | 172.0 | 58.5 |
| 8 | 161.2 | 49.0 |
| 9 | 153.9 | 46.7 |
| 10 | 161.6 | 52.5 |
| 平均 | 159.7 | 51.23 |
| 標準偏差 | 6.16 | 5.45 |
右表2は身長と体重の対応データです。このデータを用いて相関係数を計算してみましょう。
まず、共分散値sxyを計算します。エクセル関数COVARを用いて計算すると、sxy=23.7となります。
次にXとYの標準偏差sxとsyは右表のように、それぞれ6.16と5.45です。
これ...
また共分散を直接CORREL関数で計算しても、同様の値が得られることが分かります。
5.相関分析における注意点
相関が高いかどうかは、相関係数0.7程度を目安とすることが多いようです。ただしデータだけから相関係数を計算して判断することは危険です。なぜなら相関が無くても相関係数が高い値が出る場合があり、必ずグラフを描いて実測値の散布状態を確認する事が重要です。
また変数間の相関が高い場合でも、両者に因果関係があるかどうかは別の話です。例えばコンビニ件数と交通事故件数に相関があったとしたら、コンビニの数を減らせば交通事故も減ると言う考えになり妥当性があるとは言えません。人口が多い地域ではコンビニ軒数も交通事故も多くなると考えるのが妥当でしょう。
このように相関係数が高いにも関わらず両者に因果関係が無いものを偽相関(ぎそうかん)と呼びます。