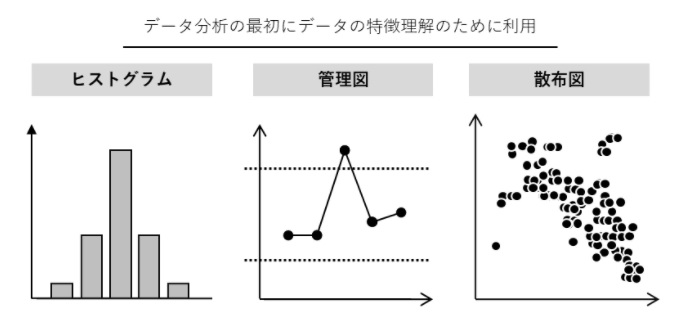
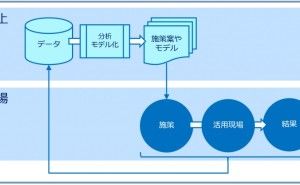
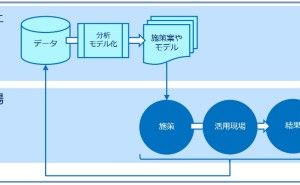
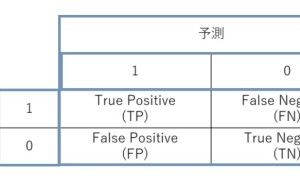
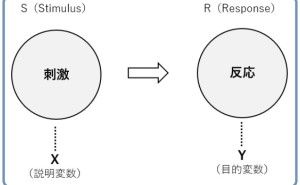
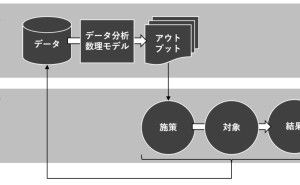
データ分析・活用に慣れていない方にお勧めなのが、次のQC7つ道具です。前回は「ヒストグラム」と「管理図」についてお話しましたが、今回は「散布図」について、概要のみ説明します。
- チェックシート
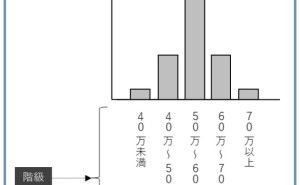
- ヒストグラム
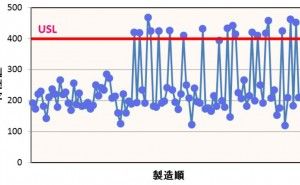
- 管理図
- 散布図 ← 今回の説明対象
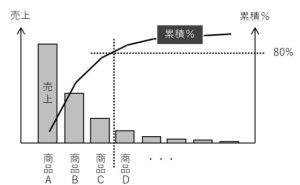
- パレート図
- 特性要因図
- 層別
前回は、上記の「ヒストグラム」と「管理図」について説明しました。7つ道具の中に、2変量(2つの定量データ)同士の関係をみる道具があります。今回は、これらについてお話しします。
1、一つの定量データの特徴を把握した次にすべきこと
ヒストグラムと管理図は、一つの売り上げや受注金額などの定量データの特徴を把握するものでした。特徴を把握したら定量データ間の関係性が気になります。
例えば……
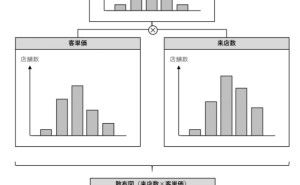
客単価の高い店舗は、来店客数も多いのだろうか?
来店客数と関係があるのは、何であろうか?
……という感じです。
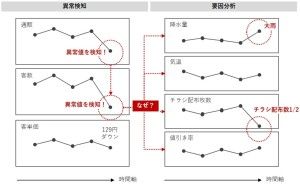
客単価の店舗は来店客数も多いのかもしれませんし、そうでないかもしれません。来店客数に影響するのは、降水量かもしれませんし、新聞の折り込みチラシの量かもしれません。定量データの特徴を把握した次にすべきは、定量データ間の関係性の分析です。
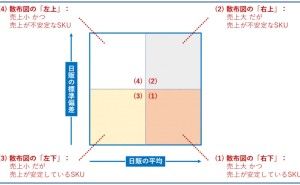
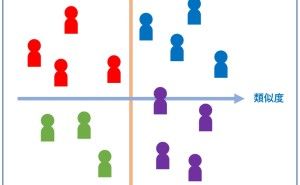
2、2つの定量データの関係は、ベタに散布図で把握
定量データ間の関係性の分析で利用するのが散布図です。誰もが一度は、使ったことや見たことはあるでしょう。
よくある使い方が……
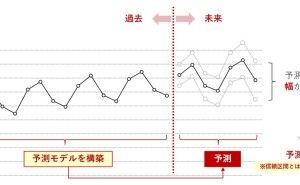
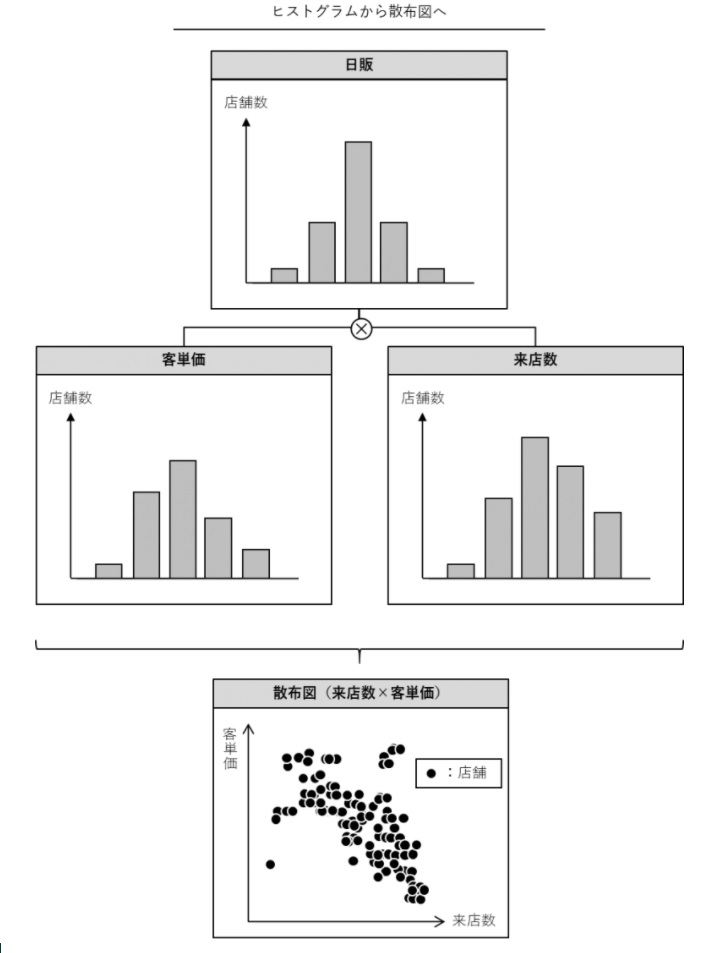
まず、ヒストグラムや管理図などで一つの定量データの特徴を把握
その後、散布図で2つの定量データの関係を把握
……という使い方です。
3、相関係数
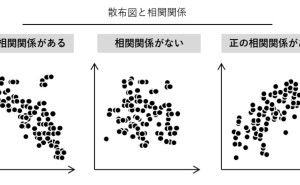
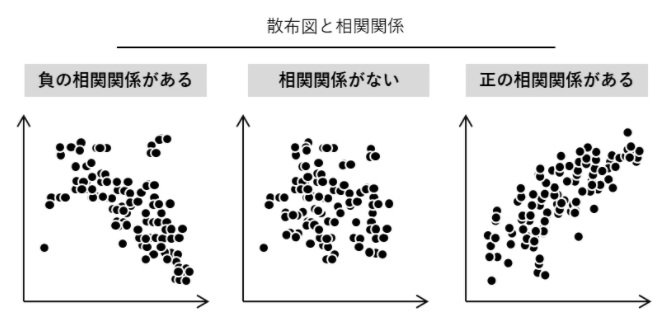
散布図を描くとき、併せて相関係数などの統計学的な指標を計算します。相関係数は-1から+1の間の数値をとります。
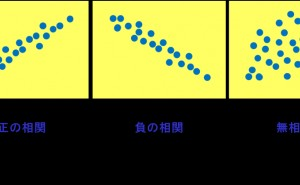
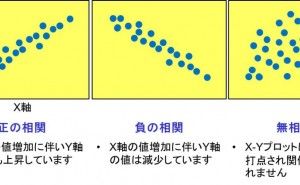
+1に近いほど「正の相関関係がある」(一方が増加すると他方も増加する傾向にある場合)
-1に近いほど「負の相関関係がある」(一方が増加しているにもかかわらず、他方が減少する傾向にある場合)
0は無相関(正の相関関係も負の相関関係もない)
(1) 相関関係は、あくまでもデータ上の関係に過ぎない
相関関係は、あくまでもデータ上の関係(厳密には線形的な関係)です。このような関係性が本当にあるのかは分かりません。そもそも因果関係ではありません。データからこのような関係が読み取れるということに過ぎません。
(2) 現場に詳しい人などと一緒に眺め解釈しよう!
相関関係は、あくまでもデータ上の関係に過ぎないため、どうなっているのかを解釈するには、現場の知見が必要です。そのため、現場に詳しい人などと一緒に、散布図や相関係数などを眺めながら、どのようなことがいえそうなのかを議論する必要が出てきます。議論の結果、現実に起こっている現象がデータに現れたものなのか、因果関係といっても差し支えないものなのかが、みえてきます。
もし、現実世界を反映したものなのであれば、その現実世界の一部をデータで表現できたことになります。
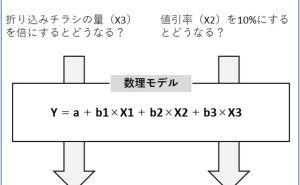
4、要因分析
散布図や相関係数などの2つ(もしくは、2つ以上)のデータの関係性を分析する手法を使い、要因分析を実施することができます。
例えば……
〇〇というアクションをしたら〇〇という結果になった
〇〇が起きると〇〇という結果になる
……とか、因果関係のようなものを、散布図や相関係数などから考えていきます。
先ほど相関係数のところでお話ししたように、データだけで行う分析からは因果関係かどうかは分かりません。因果関係どころか、そのような現象が本当に起こっているのかどう怪しいものです。
(1) へんてこな例
例えば、年収と50m走のタイムは正の相関があるといわれています。50m走のタイムが遅い(数値が大きい)ほど年収が高い(数値が大きい)のです。
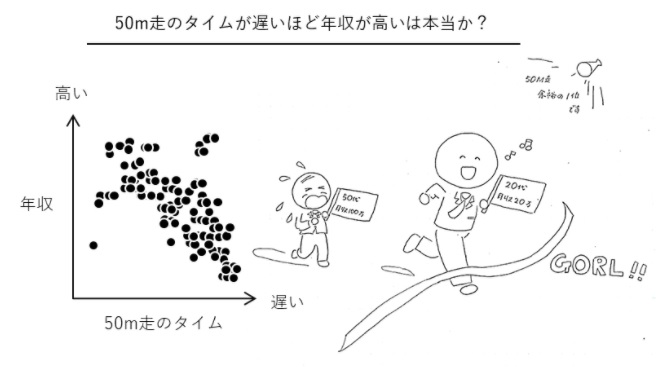
明らかに違和感があります。
実は、年収と年齢が正の相関(年齢が高いほど年収が多い)をしていて、さらに50m走と年齢が正の相関(年齢が高いほど50m走のタイムが遅い)をしているがために、年収と50m走のタイムに正の相関があるのです。このようなことはよくあります。データだけからはみえてきません。現場の人なら一発で見破れるケースが多いです。
5、データを目で見て確かめることは、データ分析の基本
要するに、前回お話ししたヒストグラムや管理図を含め、散布図などを何気なく作成し使っている方も多いと思います。データそのものの特徴理解のために使ったりします。やっていることは、データをグラフで視覚化し眺めているだけです。このようにデータを目で見て確かめることは、データ分析の基本となります。
(1) これだけで、十分にデータ活用できることも多い
実際、単なるグラフでも意図をもって見ることが重要で、想像以上に得られる情報は多いです。
例えば……
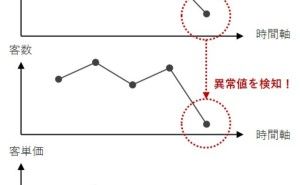
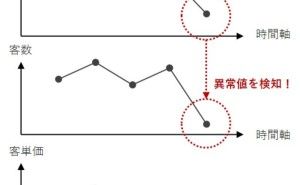
まずは、手元にあるデータに異常値がないかなとヒストグラムや管理図でデータを眺める
次に、ある2つのデータの...