統計的機械学習の世界に、2 値分類問題というものがあります。例えば、受注 or 失注、継続 or 離反、異常 or 正常、死亡 or 生存などを扱う予測モデルを構築したりします。そこで登場するのが、混同行列(Confusion Matrix)です。一時期新聞などで、新型コロナワクチンの良し悪しを評価するものとして、たまに登場していましたが、最近はあまり見なくなりました。
混同行列(Confusion Matrix) とは、統計的機械学習の2 値分類問題の分類結果をまとめた行列(Matrix)のことです。混同行列(Confusion Matrix)から、予測モデルの良し悪しを検討するための、幾つかの評価指標を作ることができます。どのような分類問題を扱うのかで、見るべき評価指標を変え選択する必要があります。
その前に、どのような指標があるのか分からないことには、見るべき指標を選択することもできません。今回は「統計的機械学習でよく使用される混同行列(Confusion Matrix)と評価指標」というお話しをします。
【目次】
1. 混同行列(Confusion Matrix)
2. 評価指標
3. 正解率(Accuracy)
4. 精度・適合率(Precision)・陽性反応適中度(positive predictive value)
5. 再現率(Recall)・感度(Sensitivity)
6. 陰性的中率(Negative predictive value)
7. 特異度 (Specificity)
8. F1スコア(F1 Score)
9. F-βスコア(F-beta Score)
10. マシューズ相関係数(Matthews Correlation Coefficient)・ファイ係数(Phi coefficient)
11. バランス正解率(Balanced Accuracy)
【この連載の前回:データ活用の成否を握るのは周辺人 データ分析講座(その295) へのリンク】
1. 混同行列(Confusion Matrix)
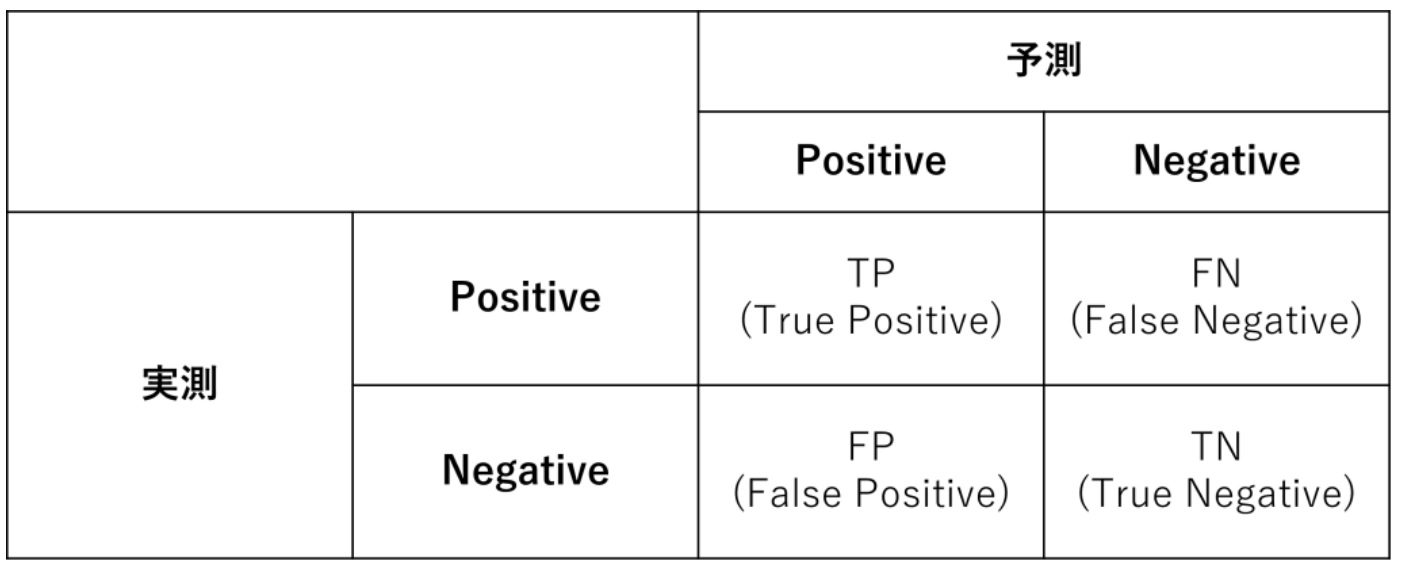
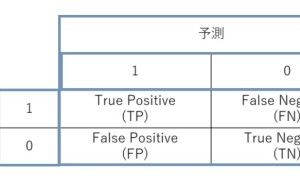
混同行列(Confusion Matrix) とは、2 値分類問題の分類結果をまとめた2×2の行列(Matrix)です。行列は4つのセルで構成されます。
- TP:真陽性(True positive)
- TN:真陰性(True negative)
- FP:偽陽性(False positive)
- FN:偽陰性(False negative)
日本語が難しいです。例えば、受注を予測するモデルであれば……
- Positive:受注
- Negative:失注
……となります。
- TP:真陽性(True positive)は、予測モデルによって正しくPositiveに分類された数です。実際の受注を、受注と予測できた数です。
- TN:真陰性(True negative)は、予測モデルによって正しくNegativeに分類された数です。実際の失注を、失注と予測できた数です。
- FP:偽陽性(False positive)とFN:偽陰性(False negative)は、予測が外した数です。
- FP:偽陽性(False positive)は、受注と予測したのに実際は失注だった数です。FN:偽陰性(False negative)は、失注と予測したのに実際は受注だった数です。
2. 評価指標
混同行列(Confusion Matrix) から、例えば以下の評価指標を計算することができます。
- 正解率(Accuracy)
- 精度・適合率(Precision)・陽性反応適中度(positive predictive value)
- 再現率(Recall)・感度(Sensitivity)
- 陰性的中率(Negative predictive value)
- 特異度 (Specificity)
- F1スコア(F1 Score)
- F-βスコア(F-beta Score)
- マシューズ相関係数(Matthews Correlation Coefficient)・ファイ係数(Phi coefficient)
- バランス正解率(Balanced Accuracy)
3. 正解率(Accuracy)
最も単純で最も分かりやすい指標です。全データの内、正しく予測できたものの割合です。
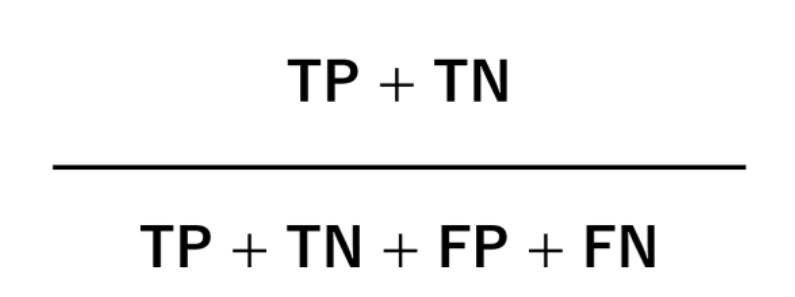
問題は、データがPositiveやNegativeのどちらか一方に偏っている場合、機能しなくなることがあります。
4. 精度・適合率(Precision)・陽性反応適中度(positive predictive value)
Positiveと予測したとき、実際にPositiveだった割合です。こちらも比較的分かりやすいかと思います。
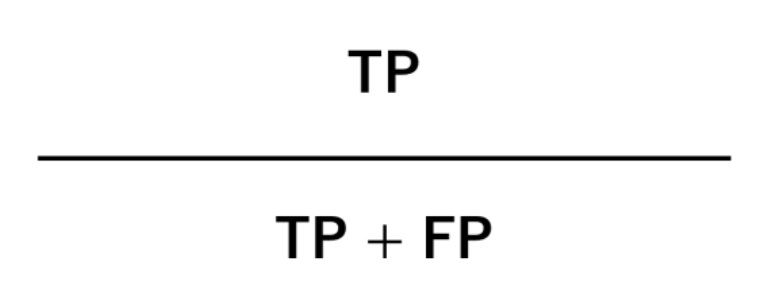
問題は、取りこぼすPositiveが、多く発生する可能性があることです。この指標はNegativeの予測精度を考慮していないため、Negativeと予測されたPositiveは蚊帳の外だからです。取りこぼしが多い場合、感度(Sensitivity)が低いと言います。
5. 再現率(Recall)・感度(Sensitivity)
こちらは、取りこぼし無くPositive なデータを正しくPositiveと予測できているかどうかを示す指標です。
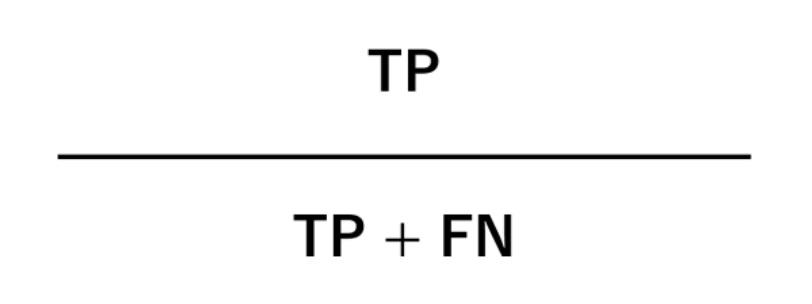
この指標が高い予測モデルを、感度(Sensitivity)が高いと言います。理想は、感度が高く精度も高い予測モデルです。しかし、この2つの指標は、トレードオフの関係を示します。精度を過剰に高くすると感度が悪化し、感度を過剰に高くすると精度が犠牲になります。
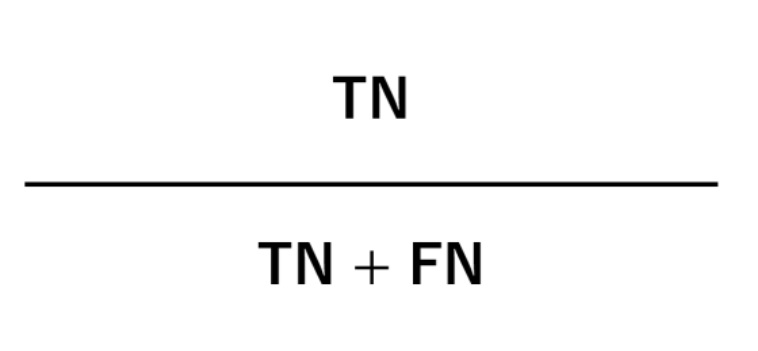
6. 陰性的中率(Negative predictive value)
Negativeと予測したとき、実際にNegativeだった割合です。こちらも比較的分かりやすいかと思います。
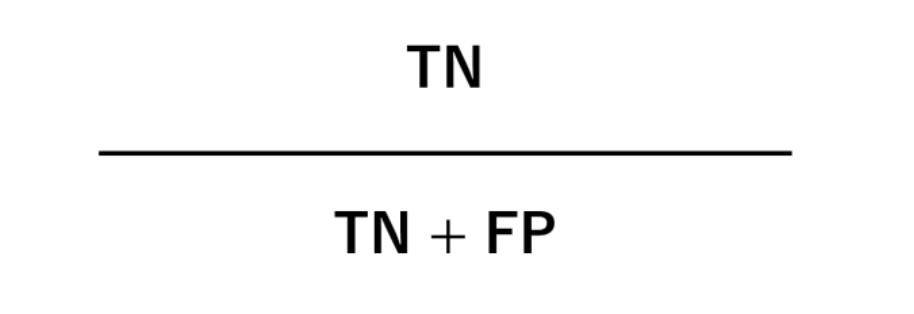
7. 特異度 (Specificity)
取りこぼし無くNegative なデータを正しくNegativeと予測できているかどうかを示す指標です。
8. F1スコア(F1 Score)
先程、理想は感度が高く精度も高い予測モデル、と言いました。この2つの指標を考慮した指標がF1スコアです。F1スコアは、精度(Precision)と 感度(Sensitivity)の調和平均です。

F1スコアの最大値は1.0で、最小値は0です。精度(Precision)と 感度(Sensitivity)のどちらも完璧な場合、最大値の1になります。精度(Precision)と 感度(Sensitivity)のどちらかが0である場合、最小値の0になります。迷ったら、F1スコアを用いるのがいいでしょう。
9. F-βスコア(F-beta Score)
F1スコアを一般化したものです。

パラメータβ(ベータ)の数値を変えることで、精度(Precision)と 感度(Sensitivity)のどちらを重視するのかを調整します。
- β=1:F1スコア
- β>1:感度(Sensitivity)重視
- β<1:精度(Precision)重視
- β=0:精度(Precision)のみ考慮
先程のF1スコアは、ベータが1だからF1スコアと言います。F2スコアといった場合、ベータが2の場合です。
10. マシューズ相関係数(Matthews Correlation Coefficient)・ファイ係数(Phi coefficient)
データがPositiveやNegativeのどちらか一方に偏っている場合、正解率(Accuracy)が機能しなくなることがあります。F1スコアなども、あまりにも極端に偏っている場合、たまにおかしくなります。そのようなデータに対し用いる評価指標として、マシューズ相関係数というものがあります。
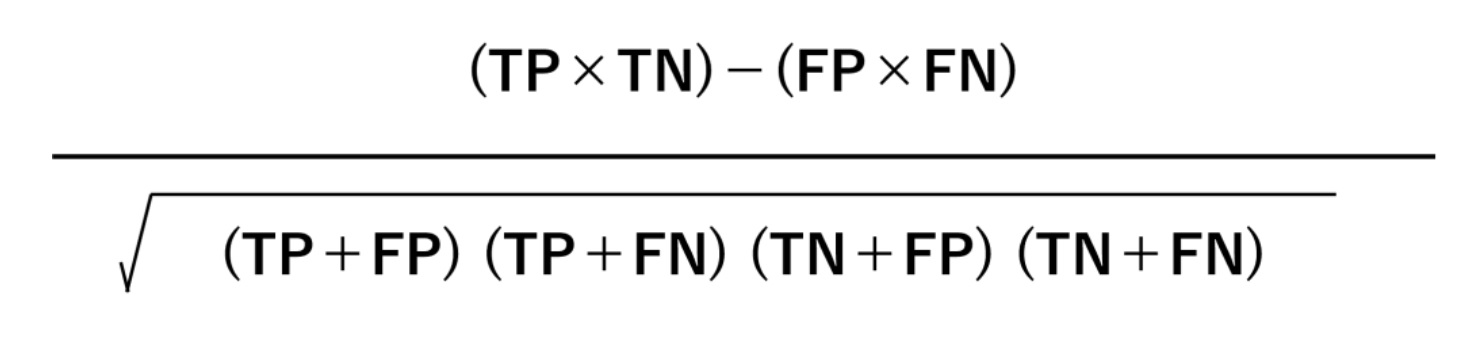
複雑そうに見えますが、Positiveを1、Negativeを0という数字を割り当てて、通常の相関係数(ピアソンの相関係数)を計算すると、マシューズ相関係数になります。マシューズ相関係数は-1から1の範囲の値を取り、予測が完璧に当たると1になり、真逆に完璧に当たると-1になります。
11. バランス正解率(Balanced Accuracy)
データがPositiveやNegativeのどちらか一方に偏っている場合、正解率(Accuracy)ではなくバランス正解率(Balanced Accuracy)を使ったほうがいいでしょう。数式もシンプルです。
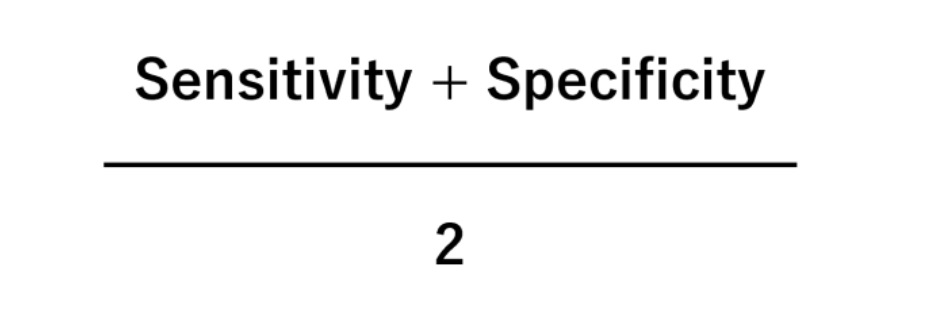
感度(Sensitivity)はPositiveの正答率、特異度 (Specificity)はNegativeの正答率です。それを足して2で割り計算します。そのことが、データがPositiveやNegativeのどちらか一方に偏っている場合にも使えるようにしています。
次回に続きます。
...