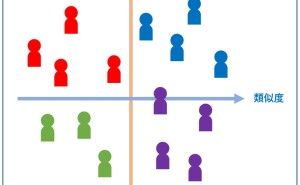
◆ 売上分析の方法や手法は、3つの「売上データの種類」で変化する
企業収益に直結するデータ分析と言えば、それは売上分析です。しかし、売上と言っても、売上金額なのか、それとも売上点数や受注件数なのか、ある顧客に対し受注するかどうかなのかで、売上分析の方法や手法は変わってきます。売上データには、いくつかの種類があります。例えば、以下の3種類です。
① 量データ
② カウントデータ
③ 2値データ
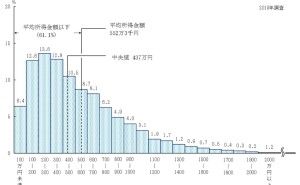
①の「量データ」とは、売上金額などの量で表現されるものです。②の「カウントデータ」とは、受注件数などの「1件、2件、3件、…」と件数などでカウントされるものです。③の「2値データ」とは、ある顧客に対し「受注した or 失注した」や「継続契約 or 契約解消」といったものです。
②の「カウントデータ」は、件数が大きい場合には、①の「量データ」と見なしても問題ないことが、統計学的に分かっています。しかし、どのくらい大きな値なら良いのかなど迷うようでしたら、②の「カウントデータ」と見なした方がよいでしょう。
今回は、回帰分析という売上分析手法の枠組みで、これらの違いを語ってみたいと思います。売上分析で迷った時の助けになれば幸いです。
1. 回帰分析という売上分析手法
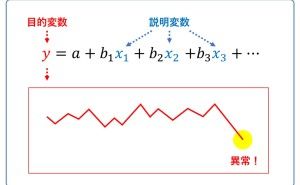
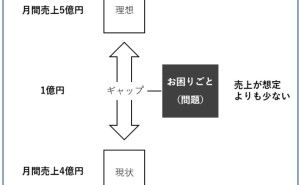
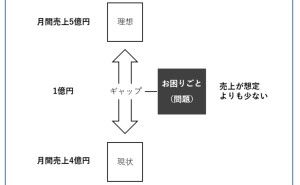
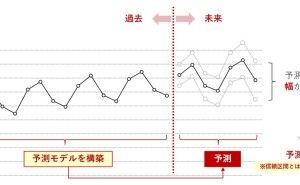
回帰分析とは、回帰モデルという統計モデルと構築することで、どのようなことが起こっていたのかを分析したり、この売上の数値は問題ないレベルなのかどうかを見極めたり、これからどうなるのかといった将来予測で使います。簡単にいうと、以下の3つです。
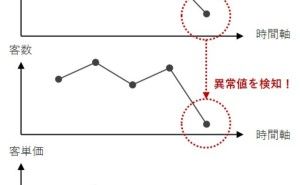
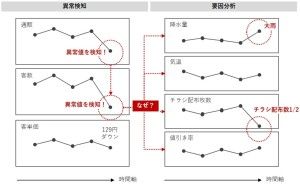
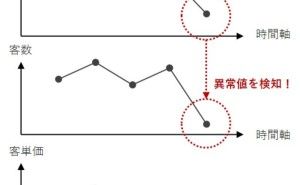
- 異常検知(この売上の数値は問題ないレベルなのかどうか)
- 要因分析(どのようなことが起こっていたのか)
- 将来予測(これからどうなるのか)
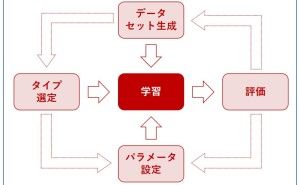
個々の深い説明はしませんが、回帰モデルという統計モデルを構築する(機械学習的には学習する)ことで、分析し将来を見通すことのできる、非常に使い勝手のよい分析手法です。さらに、普段多くの人が実施している、多くの売上分析は、回帰分析という分析手法で説明が付きます。例えば、時系列に売上の変化を分析するとき、多くの人は折れ線グラフで眺めることでしょう。一歩進めて、それを回帰分析の枠組みで分析することができます。
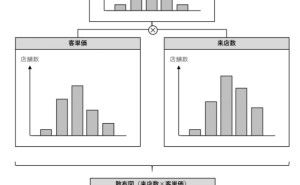
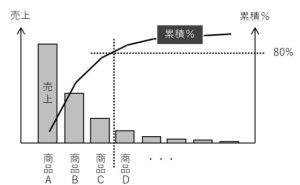
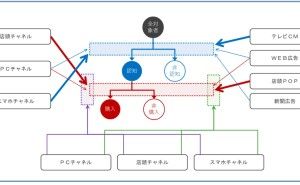
自己回帰モデルを使うことで、売上データのみで回帰モデルを作ることができるのです。自己回帰モデルを使うことで、この売上の数値は問題ないレベルなのかどうかを見極めることが、統計学的に可能です。つまり、何となくヤバそう! とか、何となく良さげ! とかという感覚的な判断以上のことができるようになります。例えば、売上を商品別やエリア別に集計する人も、多いことでしょう。
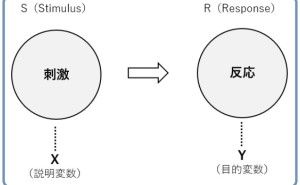
回帰分析では、目的変数と説明変数というものを設定する必要があります。売上分析の場合、目的変数は売上です。説明変数には、目的変数である売上に影響を与えるであろう変数を指定します。この説明変数に、「商品」や「エリア」を指定することで、売上の商品別やエリア別の集計を統計モデル化(回帰モデル化)することができます。統計モデル化(回帰モデル化)することで、ある商品の売上はエリアによって大きく異なる、といったことが、何となくではなく、統計学的に知ることができます。しかし、ここで1つ問題が起こります。
目的変数として指定する「売上データの種類」によって、利用する回帰モデルが異なるのです。
① 量データ ⇒ 線形回帰モデル(単回帰・重回帰モデル)
② カウントデータ ⇒ ポアソン回帰モデル
③ 2値データ ⇒ ロジスティック回帰モデル
回帰モデルには、実は多くの種類があります。ここでは、この3種類の回帰モデルについて説明します。
2. 線形回帰モデル(単回帰・重回帰モデル)
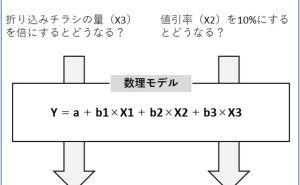
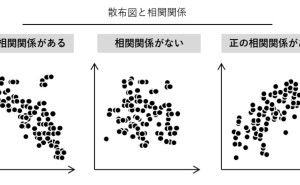
線形回帰モデル(単回帰・重回帰モデル)は、説明変数が1つのときは単回帰モデル、説明変数が2つ以上のときは重回帰モデルと言われているものです、最も一般的な回帰モデルです。xcelの分析ツールで、簡単にモデルを構築できます。例えば、新発売時の商品別の売上と販売戦力(例:販売店舗数、店舗の商品フェイス数など)の散布図(横軸:販売戦力、縦軸:売上)を描いたとき、多くの場合右肩上がりの散布図になることでしょう。多くの販売戦力を費やした商品ほど売上は大きくなるという傾向です。
この傾向を直線の数式で表したのが、単回帰モデルです。あくまでも傾向でしかないので、多くの販売戦力を費やせば確実に売上が大きくなるというものではありません。どう解釈し活用するのかは、その傾向を見る人に委ねられています。人が介在するデータ分析は、どうしても「数字を活かす力」が、その介在する人に求められます。どんなに自動化され、AI(人工知能)化されても、この「数字を活かす力」は求められ続けると思います。
さらに説明変数として、リスト件数(見込み顧客数)や顧客の属性(例:一般消費者であれば性別・年代など、法人顧客であれば業界・企業規、模など)、商材カテゴリー、そのカテゴリー市場規模、市場の伸長率、市場シェア、広告プロモーションの有無などを説明変数として追加し、線形回帰モデルを構築することができます。説明変数が2つ以上の重回帰モデルです。
重回帰モデルもあくまでも傾向値ですので、どう解釈し活用するのかは、その傾向を見る人に委ねられています。他には、小売店であれば目的変数を来店客数やレシート枚数(売上件数)にしてもよいでしょう。ECサイトであれば、サイトへの訪問数やカート投入数など、購入以外の件数を目的変数にしてもよいでしょう。
線形回帰モデル(単回帰・重回帰モデル)の特徴として、目的変数である売上が「量データ」でなければならないところにあります。多くの場合、売上金額を目的変数としていれば問題ないことでしょう。売上点数や受注件数などは、若干微妙で、「量データ」といよりも「カウントデータ」です。
このとき気を付けなければバラないのは、「人」や「回」や「件」といった単位は、厳密には「カウントデータ」になります。ECサイトや小売店などの、訪問者数や来店顧客数、売上点数などは、非常に大きな数字になる可能性があるため、線形回帰モデル(単回帰・重回帰モデル)でも問題ないかもしれません。
3. ポアソン回帰モデル
先ほども申しましたが、「人」や「回」や「件」といった単位は、厳密には「カウントデータ」になります。この場合、線形回帰モデル(単回帰・重回帰モデル)ではなく、ポアソン回帰モデルを使います。ポアソン回帰モデルは、線形回帰モデル(単回帰・重回帰モデル)に比べ聞きなれない人も多いと思います。
ポアソン回帰モデルの説明変数の多くは、レシート枚数(売上件数)や売上点数、購買者数、受注件数などになります。金額ではありません。他には、ECサイトの訪問数やカート投入数、小売店の来店者数、企業への問い合わせ件数なども、カウントデータになります。このようなデータを目的変数に指定するとき、ポアソン回帰モデルを使います。
ポアソン回帰モデルでやっかいなのは、Excelなどで手軽にモデル構築できないことにあります。Excelの分析ツールは、単回帰や重回帰と言った回帰モデルしか作れません。Excelで強引にポアソン回帰モデルを作ろうとすると、Excelのソルバーを使わなければなりません。次に紹介するロジスティック回帰モデルも、Excelのソルバーで回帰モデルを構築することができます。
説明変数は、線形回帰モデル(単回帰・重回帰モデル)と同様に指定すればよいので、分析そのもののやり方は大きく変わりません。さらに、来店者数や問い合わせ件数などの、数字が多くくなるものは、線形回帰モデル(単回帰・重回帰モデル)でもよいため、ポアソン回帰ではなく線形回帰モデル(単回帰・重回帰モデル)で構築してしまえば、それはそれでよいかもしれません。
しかし、問題があります。来店者数や問い合わせ件数などの数字が多くくなるものは、線形回帰モデル(単回帰・重回帰モデル)でもよいと言いましたが、例えば店舗別や商品別、時期別、時間帯別のように、売上データを細かく分析するとき、来店者数や問い合わせ件数などの数字は小さくなります。
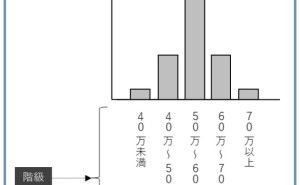
例えば、全国で年間40万人ぐらい来店し購入するが、各店舗の1日単位で考えると5人ぐらいしか購入しない。自動車や不動産などの高額なものであれば、もっと数字は小さくなりと思います。このようなとき、全国レベルでは線形回帰モデル(単回帰・重回帰モデル)を使えても、各店舗レベルではポアソン回帰モデルということになります。いっそのこと、どちらかにそろえた方が良いでしょう。
4. ロジスティック回帰モデル
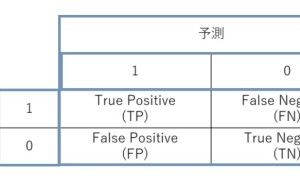
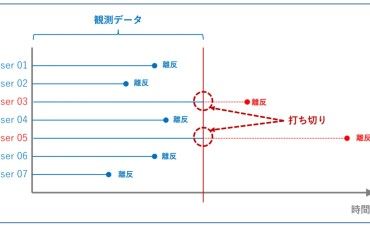
ロジスティック回帰モデルは、目的変数が「2値データ」の場合に使います。「2値データ」とは、ある顧客に対し「受注した or 失注した」や「継続契約 or 契約解消」といったものです。
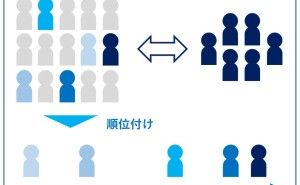
受注分析や離反分析をするとき、必須の分析になります。説明変数は、線形回帰モデル(単回帰・重回帰モデル)と同様に指定すればよいため、分析そのものはやり方は大きく変わりませんが、より一人ひとり、もしくは、より一件一件(1社1社)の分析をすることになります。
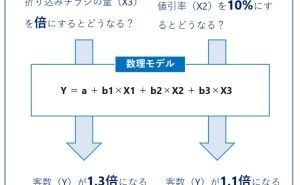
例えば、ロジスティック回帰モデルで分析することで、受注要因や失注要因、継続要因、離反要因などを分析することができます。さらに、受注要因を変化させる施策をすることで、どの程度受注確率を変化させられるかが分かります。ロジスティック回帰モデルの特徴として、「受注 or 失注」ということだけでなく、受注率(or 失注率)といった確率で分析することができることが、あげられます。
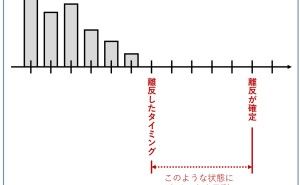
正確には、受注分析であれば受注率、離反分析であれば離反率というものを、ロジスティック回帰モデルで統計モデル化します。その後、例えば、受注率が0.5以上であれば受注と見なそうとか、離反率が0.5以上であれば離反と見なそうとか、そのように考えます。そのため、〇〇率(例:受注率、離反率)のどこを閾値(例では0.5)にするのか、という問題が起...