◆ データ分析・活用と数理統計学的な厳密性との狭間で
データ分析やデータサイエンス、機械学習などの基礎的なバックボーンとして、数理統計学に関するある程度の知識は必須です。しかしデータ分析・活用を目指すなら、数理統計学的厳密性は放棄したほうが良さそうです。今回は「データ分析・活用と数理統計学的な厳密性との狭間で」というお話をします。
1. 数統計学的な判断をデータ分析に組み込む
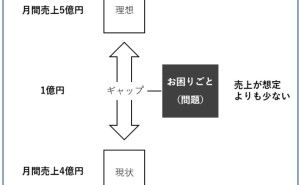
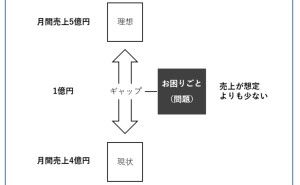
データ分析・活用を考えた時、その中で統計学的な判断をデータ分析に組み込むことをよく考えます。
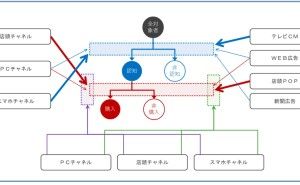
統計学的な判断とは、次のようなデータによる意思決定支援です。
- 対前年比で売り上げはどうだろうか?
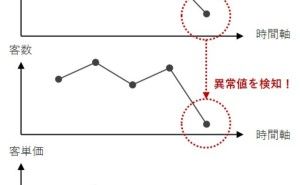
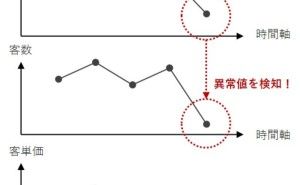
- 今日の売り上げは、通常と比べ悪いといえるのだろうか?
- 先週行ったキャンペーンの影響はどうだろうか?
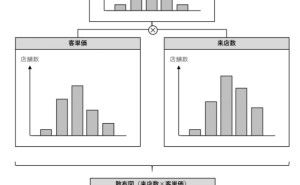
- 売り上げに効いている要因として、何が考えられるだろうか?
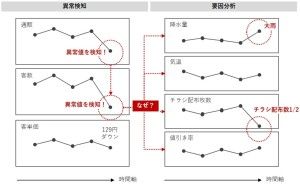
- 先日の土・日の売り上げが悪かった要因は、何であろうか?
- 何の対策を打たないまま営業すると、来月どうなりそうか?
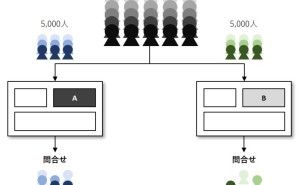
- A案とB案、どちらがいいだろうか?
2. 厳密性を追求したあのころ
私が20代のころ、数理統計学的な厳密性を最大限に考慮したデータ分析を試行したことがありました。いたずらに時間だけが過ぎ、骨の折れるものでした。工夫次第でどうにかなりそうで、どうにもならないものでした。現場のスピード感に合わせるためには、どこかで厳密性の追求を放棄する必要が出てきました。
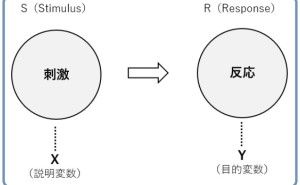
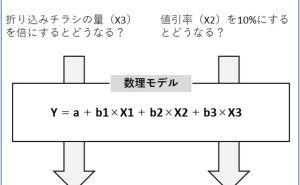
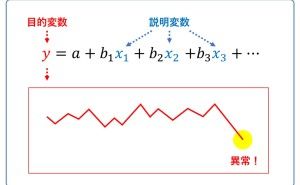
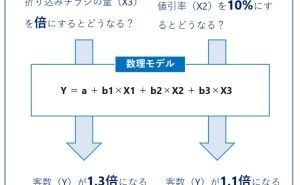
(1) 回帰分析
データ分析・活用で、よく登場するものに回帰分析というものがあります。手法の紹介やツールの使い方を説明した、データ分析やデータサイエンス、機械学習などの入門書に、必ず登場する分析手法です。回帰分析については、これ以上説明はしません。よく目にする分析手法だということだけ、ここでは知って頂ければと思います。
3. 数理統計学的厳密性を満たすのはほぼ不可能
回帰分析は、厳密には独立性・等分散性・正規性・線形性などの条件を満たす必要があります。これらの条件の話も、ここでは説明しません。ここで言いたいのは、ビジネスの現場で発生するデータは、これらの条件を満たすことは皆無だということです。実際は、工夫次第でこれらの条件に近づくことは可能です。
しかし近づくだけで条件を十分に満たすことはありません。
(1) 明らかに条件を逸脱していない限り、実務的にはいいのではないか
言いたいことは「明らかに条件を逸脱していない限り、実務的にはいいのではないか」ということです。したがって実務的には数理統計学的...