1.散布図の概要
前回のQC7つ道具、その4 管理図に続いて解説します。散布図とは、同一条件下で採られた2つのグループのデータを、それぞれX軸とY軸にプロットする事により、両者の関係を示した図です。散布図は2群に相関関係があるか、あればどの程度の関係にあるかを確認する事を目的としています。
相関がある場合に片方の特性値が分かれば、もう片方の特性値範囲を予測する事が出来ます。相関度が高ければXの値を一定範囲にコントロールする事により、Yの値も一定範囲に制御する事が出来ます。またプロットした点が異常値であればすぐに気づくことが出来ます。
例えば体重をYとして、Xを身長、胸囲、腹囲と変えてそれぞれの散布図を描けば、どのXが最も体重と相関が高いかが散布図を観て分かると思います。
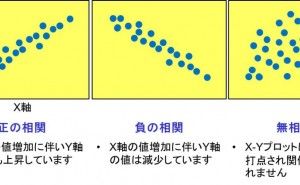
・X-Y相関のパターンとして
Xが増加すればYも増加する右上がりの正の相関
Xが増加すればYは減少する右下がりの負の相関
X-Y間に関係性が観られない無相関
の3つがあります。
図1、散布図
2、散布図の注意点
注意点としては、一見無相関に見えても、層別を行った後に再度散布図を描けば相関が出てくるケースが多々あるという事です。例えば、研磨時間Xと研磨量Yに相関が観られなかったとします。 それを研磨装置で層別して、それぞれ散布図を描くと相関が観られる場合です。
相関度の高さを見る指標として、相関係数があります。相関係数の絶対値が1に近いほど相関が高く、両者の関係は直線に近くなります。 目安として0.7以上あれば相関があると言えます。
ただし相関有無は、相関係数のみで判断してはいけません。 直線関係に無い点の分布でも相関係数が高い場合があります(下右図参照) 、異常値に影響されて相関が低くなったり、逆に少ないデータで計算した相関係数が高かったりと実用には、注...
図2、散布図異常パターン
3、散布図異常パターン
X-Yの相関の詳細については相関分析という手法で解析が出来ます。 また複雑な実プロセスにおいては散布図で高い相関が得られるような単純なケースは少なく、特性Yに対して複数の要因Xの関係性を観る多変量分析と言う手法があります。