今回は、統計手法の一つである「回帰分析」の解析事例を解説します。
事例として、ほぼ同じタイミングで製造を開始した製品(約200個)に現時点での完成率のデータがそれぞれあります。この完成率のデータを元に「完成率が高いグループ」と「完成率が低いグループ」の2グループに分けて、それぞれ例えば50個(50製品)ずつ抜き出して、2つのグループに(完成率以外に)製品にどんな特徴(完成率の高低に影響を与えた要因)があるかを大まかにみるという事例です。この目的は、完成率に影響を与えた(かもしれない)要因として、どんなものがあるのかを把握して、完成率の向上に役立つ情報を得たいというものです。
1. 「回帰分析」の適用例
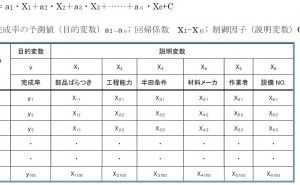
条件として、「完成率」が数値化されていることが前提になります。本事例では100個の製品毎の完成率が数値化されていることを前提にします。表は目的変数(完成率;y)と説明変数(X1~X6)のデータ一覧表になります。このデータを使用して回帰分析すると以下の線形方程式得られます。
2. 制御因子の選定
重要なのは、制御因子を決める事になります。例えば、次のような因子になります。
計量化できる因子では、部品のばらつき、工程能力、製造条件(半田付け条件等)他、計数化できる因子は材料メーカ、作業者、設備No.などが考えられます。計量値、計数値に関わらず、完成率に影響を与える因子をリストアップします。計数値は材料メーカA、B二社あれば、0,1などの計数値を入力します。
基本原理は最小二乗法により実測値と上記回帰式との誤差を最小になる回帰係数a1~a6を決める作業です。計算はいたって簡単です。
エクセルのアドインにある「データ分析」ツールを使用します。瞬時に回帰係数は求めることができます。計算結果は四つの表がアウトプットされます。この結果より
- 寄与率 回帰式のあてはまりを検証 (相関係数の二乗)
- 回帰の有意性 誤差に対して回帰係数が有意であることの検証
- 回帰係数の有意性 回帰係数がばらつき内で0にならないことを検証
- 残渣の検証 実測値と予測値の差の検証
上記4点を検証する事が鍵になり、若干のスキルが必要になります。入力値はこの場合、yの完成率 完成率高い低いに関係なく100データ、xは制御因子を6とすると600データとなります。
- 寄与率は一般的には70%以上であれば回帰の当てはまりが良い
- 回帰の有意性は信頼率95%で誤差に対して有意である
- 回帰係数の有意性は信頼率95%で回帰係数が0になる場合には、該当の制御因子は因子から除去して再度回帰分析を行います。制御因子はできるだけ少ないほうがベターです。
- 100の完成率デー...
タの標準残渣が3倍の標準偏差を超える場合にはそのデータの再確認を行います。
3. 完成率を回帰式でシミュレート
今回の事例では、完成率の高い製品を製造する事が目的です。求めた回帰式から回帰係数aの絶対値が大きいほど目的変数 y ̂ への影響が大きくなります。従って、その回帰係数aを有する説明変数xによってコントロールすることが結論です。当然、コントロール可能な制御因子とできない制御因子があります。その時には他の制御因子との最適組み合わせを指向することになります。結論は完成率を回帰式でシミュレートできることです。つまり、製造プロセスを開始する前に完成率を予測できることです。