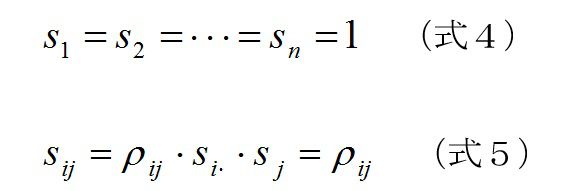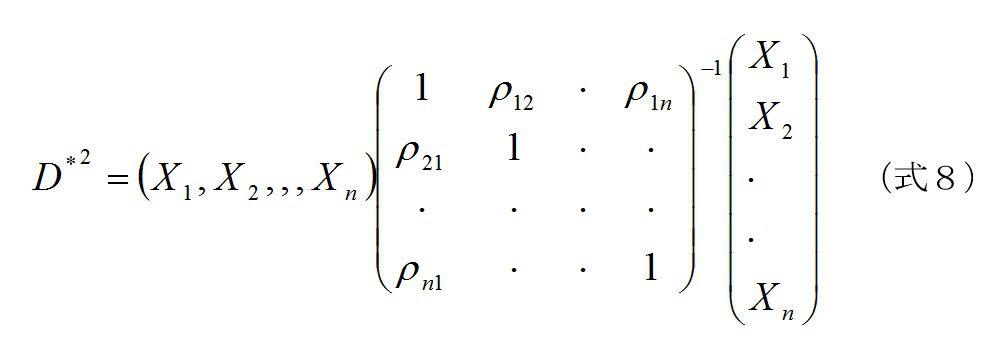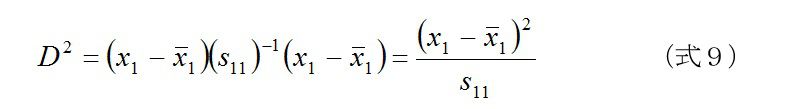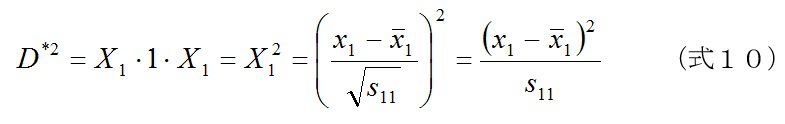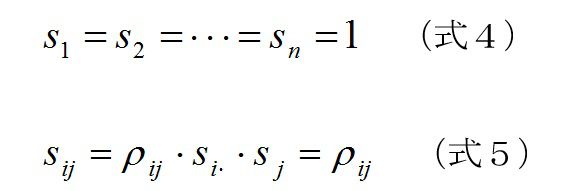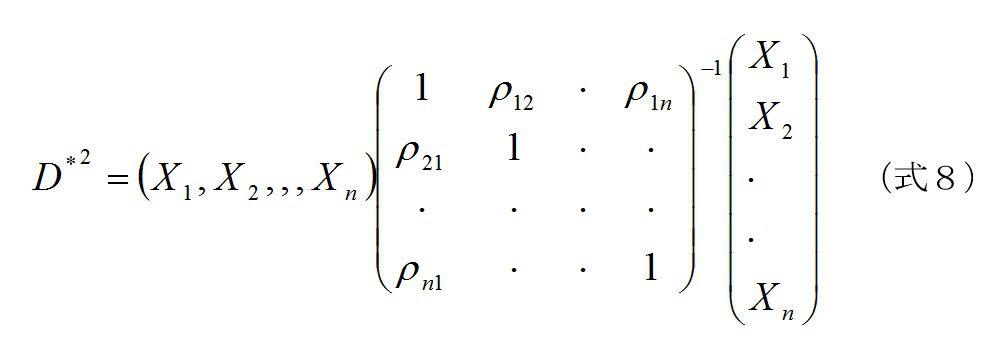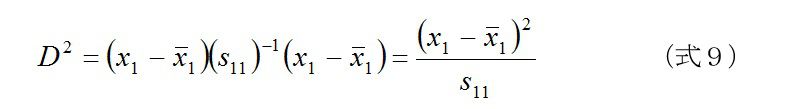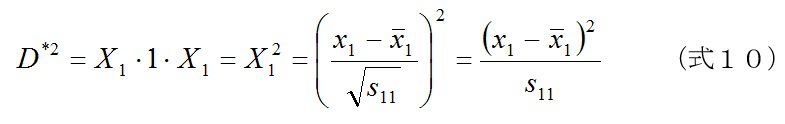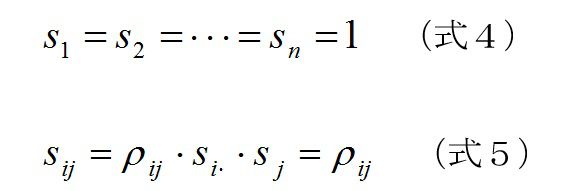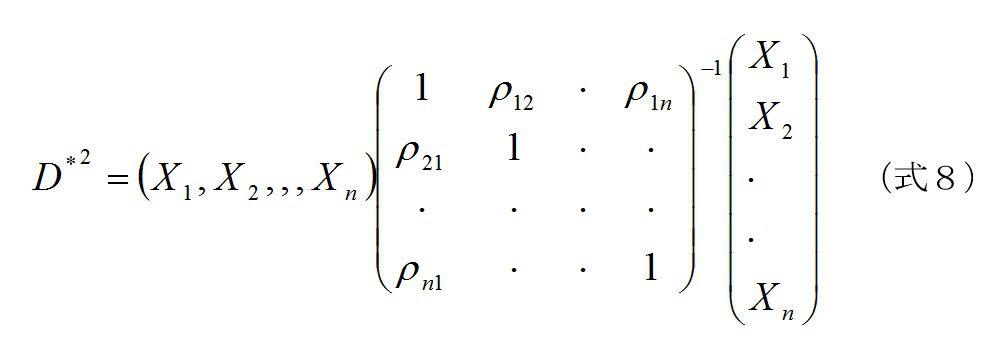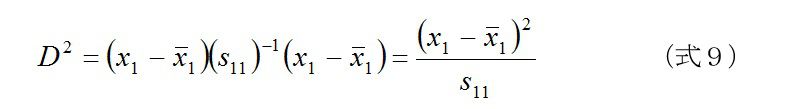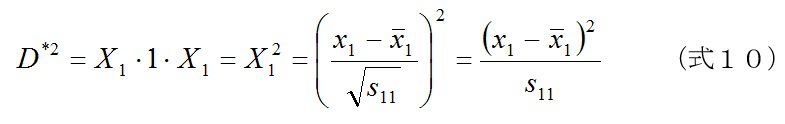分散・共分散行列でマハラノビス距離による解析指導をしていた企業で相関行列でも同じなので、エクセルならこの方が簡単という話をしました。ところで、そこの技術者から、二つの質問を受けました。ひとつは、なぜそうなるのか? 二つ目は同じならどちらか一つの式でいけないのか? ものの本に、二つのやり方をわざわざ書いてあることも多く、この辺の事情を説明します。
まず、相関係数の定義からです。分散や共分散の基本はネットやテキストにありますので省略したいのですが、ただし、記号はまちまちです。sと書いてある場合が多いように思いますが、変動のS(これを自由度で割ったものがs)と間違えないようにしましょう。間違えても自由度が分子分母で消えてなくなるので実害はありません。変数iとjの相関係数は、式1で定義されます。sijを共分散、siiやsjjを分散、その平方根をsi, sjとして
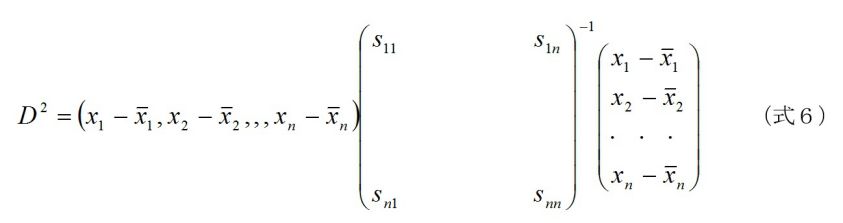
ここでデータを標準化しますと、よく知られているように平均がゼロ、標準偏差が1になるので、下記のように共分散は相関係数になります。
式5は式3を右から左に見た場合に納得します。標準化されたデータの分散・共分散行列が相関行列に等しいということです。ここで、マハラノビス距離を算出する際のことを考察します。分散・共分散行列からスタートする場合、以下のようになります。
ここで、xiを標準化すると、標準化された変数をXiとして
これの分散・共分散行列は、以下のようになります。
標準化されていますから平均ゼロ、分散1(標準偏差1)、共分散=相関係数(式5)を代入しますと
マハラノビス距離は、データの標準化によって、相関行列を用いて計算できることになります。問題は、分散・共分散行列からスタートの式6と相関行列を使った式8の値が異なるかどうかです。逆行列の部分を普通の数値(スカラー)と考えて、置き換えると、なんとなく同じ値になりそうだと思われます。この推察は正しいです。まず、1次(1変数)の場合で、みてみます。分散・共分散行列からのマハラノビス距離は、式6より
相関行列からのマハラノビス距離は、式8より
よって、分散・共分散行列でも相関行列でもマハラノビス距離は等しくなります。2変数の場合、今度は逆に相関行列から計算します。計算しやすいからです。式3~8から
式13と式23は等しい。よって、二次元の場合にも、相関行列によるマハラノビス距離と分散・共分散行列によるマハラノビス距離は等しくなることがわかります。n次元の場合にもこれが成立することがわかっていて、どちらを用いても同値です。
よって、MT法や判別分析におけるマハラノビス距離はどちらでもよいのです。ただし、エクセルを用いてこれらの手法を使う場合には相関行列スタートがよいです。理由は下記によります。
1.エクセルでは相関行列が簡単に作成される。(分散・共分散行列は簡単にはできない。)
2.その相関行列をつかえば相関係数の高いものを容易に選び排除できるので多重共線性を予防できる。
3.分散・共分散の計算では、共分散の場合、単位の違いやデータ桁数の違いがあると、大きな数値範囲
のものに影響を受ける。数値範囲が小さいと桁落ちにより、効果が隠れてしまう。(これはエクセル
でなくても起...