前回のクラスター分析に続き、今回は主成分分析について解説します。
1. 主成分分析 ~ 多くの特性(情報)を1個に集約
総合と分類に役立つ手法として、主成分分析があります。
学力テストを例に解説します。科目は英数国、全教科100点満点とすると3教科合計は300点です。それでは、合計点の高い人は総合学力が高いかどうかについて考えてみましょう。
総合学力=合計点で良いかどうかです。この方式では、文系の人は得をします。というのも、英語と国語には通常、高い正相関があり、合計点では文系の人が得をする(高い評価)結果となります。極端なことをいえば、英語と国語に相関係数1.0が成立していたら、文系能力をダブルカウントした総合学力になります。
Aさんは数学が0点でも、英語と国語が50点、Bさんは数学が50点で英語と国語が25点、Cさんは数学が100点で、英語と国語は0点ですが、みんな合計は100点です。しかし、英語と国語に高い相関(極端ですが、1.0と仮定)があるのなら、ダブルカウントになった分を補正する必要があります。要は、英語と国語の得点に0.5をかけるのです。そうすると、Aさんは数学0点、英語と国語で25点ずつとなって、合計50点。Bさんは75点です。Cさんは合計100点のまま。相関を考慮すると、総合学力としてはC,B,Aの順です。
この場合の総合学力は、
数学の点数+英語の点数×0.5+国語の点数×0.5
としたわけです。この総合性をもう少し、厳密に計算して総合力みたいなものを算出しようという考えが、主成分分析の大きな目的の一つになります。そして、これは見方を変えると、総合力の表現式さえ分かれば、いちいち個別の点数を気にしなくて良いため、管理が簡単になるのです。多くの特性(情報)を1個に集約したようなもので、これを主成分といいます。
また、総合力だけでなく、理系向きか文系向きかといった解析も可能になります。先の総合力を第一主成分とすれば、これは第二主成分として算出できます。これらの計算には、分散・共分散行列あるいは相関行列に加えて行列、固有値、固有ベクトルの知識が必要です。エクセルしかない場合は、次のようにやってみてください。
- 計算したいデータの分散・共分散行列を求める
- その固有ベクトルを求める→これが係数に該当
数理的な概念を2個の変数で、グラフ的に説明すれば下図のようになります。
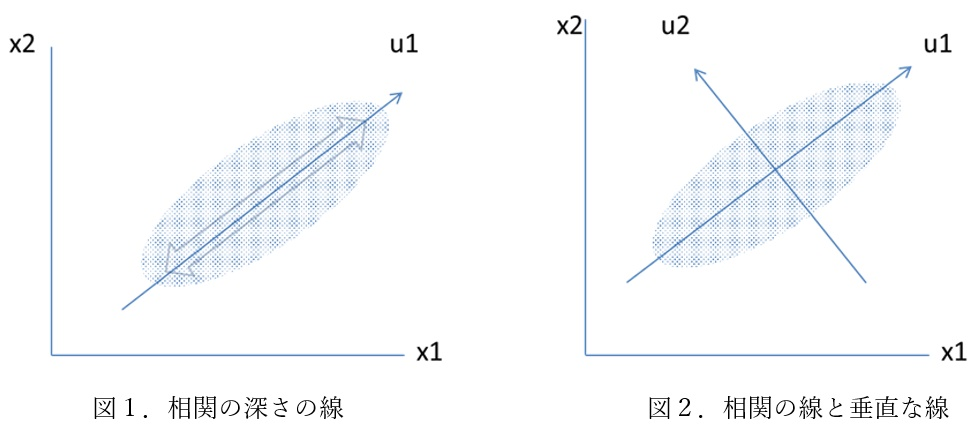
x1とx2の情報は一義的、つまり総合的にはu1の線で説明できます。つまりx1とx2の情報をu1という線形式一つで説明できます。これを第1主成分といいます。大抵の場合、総合力、総合性を示します。図2はu1に対して、垂直な線u2ですが、u1では説明しきれなかった情報を説明する線です。これを第2主成分といいます。
2. 主成分分析の手順
もう少し、現実に近いデータに切り替えて説明しましょう。
3教科の点数を下記のようになったとして、主成分分析を実行します。
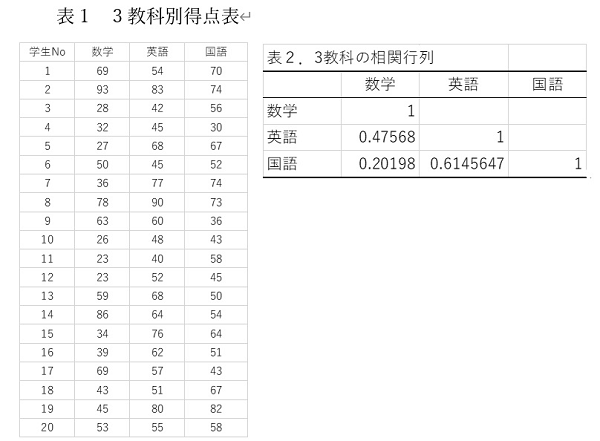
数学、英語、国語に添え字1~3を対応させて、
第一主成分の得点式は、
z1i=-85.3379+0.8426xi1 + 0.4547xi2 + 0.2885xi3 式1
第二主成分の得点式は、
z2i=45.7261+0.5074xi1 - 0.4911xi2 -0.7080xi3 式2
式1は、最初の定数は別にして、係数の大きさに注目しましょう。
z1i=-85.3379+0.8426xi1 + 0.4547xi2 + 0.2885xi3
青字は数学に、赤字は、英語、国語に対応しています。文系科目が2科目あるので、小さな係数をかけて数学とのバランスをとっているのです。そうしないと、文系が得意な人が「得」をするからです。よって、合計点数だけなら理系は不利になりますが、式1を使えば、学力の総合的な評価ができることになります。これが第一主成分の意味です。
式2では、係数の正負に注目しましょう。
z2i=45.7261+0.5074xi1 - 0.4911xi2 -0.7080xi3
正の係数は、数学に対応しています。逆に、負の係数は英語と国語です。これらのことから、式2、第二主成分は、文科系得意と理科系得意に分かれているという解釈ができます。つまり、第二主成分の値が大きいときは理系向き、小さいときは文系向きです。
科目を増やすと、第3、第4が出る場...