♦ すべり系とシュミット因子
金属材料はすべり運動によって塑性(そせい)変形が起きます。
そしてすべり面は最密充填構造です。結晶構造によってすべり系の数は異なります。体心立方格子が48個、面心立方格子が12個、稠密(ちゅうみつ)六方格子は3個です。一般にすべり系が多いほど塑性変形しやすいのです。
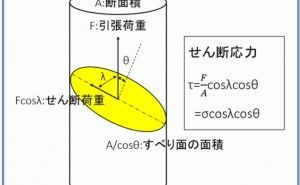
図1.丸棒に働くせん断応力
図1、断面積Aの単結晶の丸棒に引張荷重Fが負荷された時を考えます。材料には軸方向に応力が負荷されますが、塑性変...
形が起こるためには、すべり面にせん断応力
τ が作用して、すべり運動を起こすことが必要です。
すべり運動は丸棒の垂直断面から、ある角度のすべり面で起こります。ここで λ はすべり面と引張荷重の角度、θ はすべり面の法線と引張荷重の角度です。引張荷重のうちすべり面に負荷される荷重は Fcosλ となり、すべり面の面積は A/cosθ となります。この荷重を面積で割ることでせん断応力が求められます。これを式(1)に示します。
τ=F/Acosλcosθ=σcosλcosθ (1)
σ は引張応力です。cosλcosθ はシュミット因子と呼ばれ、最大値は λ=θ=45° すなわち 0.5です。すべり系の中でも大きなシュミット因子を持つすべり系を主すべり系と呼びます。シュミット因子により、丸棒に引張応力を負荷した場合、最大のせん断応力は斜め45°の向きに働くことを表します。
次回に続きます。