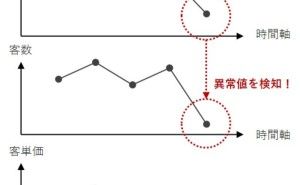
単純な売上データも、ウェブサイトのアクセス状況も、工場などのセンサーから収集すされるデータも、時系列データです。多くのビジネスの現場で発生するデータは、「時間軸」の概念の付与された時系列データです。ビジネスの現場でデータ活用を始めるとき、この最も目にし易い時系列データで何をすればいいのか、という問いが襲ってくることでしょう。多くの場合、時系列データを折れ線や棒グラフで表現しモニタリングするようです。
今回は、「異常検知は最も始めやすいデータ活用の1つ」というお話しをします。
【目次】
1.時系列データを折れ線や棒グラフで表現しモニタリング
(1)時系列の異常検知モデルで使うデータはシンプル
(2)異常検知のプロセス
(3)予測点と予測区間
2.よく使われる時系列モデル
3.異常の偽陰性(通知されない)を減らしたい
1.時系列データを折れ線や棒グラフで表現しモニタリング
ビジネスの現場でデータ活用を始めるとき、時系列データを折れ線や棒グラフで表現しモニタリングするケースが多いと感じています。ただ、モニタリングするだけだと、「数値が上がった下がった」ということを主観的に感じ、問題が起きているならば対策を打つ、ということをすることでしょう。ここで、モニタリングする数値の種類が多くなると、「数値が上がった下がった」ということを1つ1つ主観的に感じ、問題が起こっているかどうかを把握するのが、難しくなったり面倒になったりします。
そうなると、気が向いたときにしか見向きのされない折れ線や棒グラフが単に存在するだけ、ということになることでしょう。そこで、登場するのが異常検知というデータ活用です。モニタリングしている数字の異常を検知してくれます。
(1)時系列の異常検知モデルで使うデータはシンプル
時系列データの異常検知で使うデータは非常にシンプルです。例えば、次のような1変量のデータ(例では、月別の乗用車の販売台数)でも、できます。
数理モデルの世界で言うところの「目的変数Yだけ」(売上などの着目している指標)という感じです。扱うデータが非常にシンプルなため、今からでも始められるデータ活用です。
もちろん、異常検知の数理モデル(多くの場合、時系列の統計モデル)に「説明変数X」(着目している指標に影響を与える特徴量)を加えても問題ありません。
(2)異常検知のプロセス
異常検知のプロセスは、非常にシンプルです。
- 過去データを使い異常検知で使うモデルを構築し正常なの範囲(閾値)を予測
- 観測値がこの正常な範囲(閾値)から外れている場合に異常なアクティビティとして通知
異常検知で使う数理モデル(多くの場合、時系列の統計モデル)は、異常検知の対象データの前の過去データを使い構築した数理モデル(多くの場合、時系列の統計モデル)です。
その数理モデル(多くの場合、時系列の統計モデル)を使い、異常検知の対象となるデータを予測(通常は点と区間)し、異常検知の対象となるデータの実測値(実際の値)がその予測から大きくズレている場合に、異常が起こったと判定します。過去データで構築した数理モデル(多くの場合、時系列の統計モデル)は、過去の状況(データのパターンなど)を数理モデル(多くの場合、時系列の統計モデル)で表現したものです。
過去と大きく異なる何かが起こった場合、過去の状況を表現した数理モデル(多くの場合、時系列の統計モデル)では表現しきれず、予測(通常は点と区間)から大きくずれます。
(3)予測点と予測区間
数理モデル(多くの場合、時系列の統計モデル)で予測されるのは、点(特定の値)の場合と区間の場合があります。通常、多くの人がイメージするのは点(特定の値)の予測でしょう。時系列の統計モデルの場合、点(特定の値)の予測だけでなく区間の予測(予測区間)をすることができます。
似たような用語に、信頼区間というものがありますが、全く別物です。
2.よく使われる時系列モデル
例えば、次にような数理モデル(多くの場合、時系列の統計モデル)がよく使われます。
- 指数平滑化法
- 移動平均法
- ARIMAモデル
- Prophetモデル
- 状態空間モデル
- 回帰型ニューラルネットワークモデル
指数平滑化法や移動平均法は、Excelなどで簡単にできます。
伝統的には、ARIMAモデルがよく使われます。ARIMAモデルそのものは、政府系のマクロ指標(日本だけでなく米国や欧州などでも)などで季節調整などで積極的に活用されています。ARIMAモデルは、モデル構築手順がほぼ完成されており、自動でARIMAモデルを構築するアルゴリズムもあり非常に使い勝手が良いですが、モデル構築にある程度の期間の長さが必要になります。
ARIMAモデルに限らず他の時系列系の数理モデルも、モデル構築にある程度の期間の長さが必要になります。データ期間が長いほうがいいです。季節性を考えると3年以上は欲しいとことです。そのような中、モデル構築に必要なデータ期間が短くても何とかなるのが、一番最初に言及した、指数平滑化法や移動平均法です。指数平滑化法と移動平均法を比べるなら、移動平均法の方がいいでしょう。
3.異常の偽陰性(通知されない)を減らしたい
先ほど、「異常検知のプロセス」のところで、「観測値がこの正常な範囲(閾値)か...
「偽陰性率」(False Negative Rate、本当は異常なのに異常でないと判定される割合)を小さく抑えると、「精度」(Precision、適合率、異常と予測したとき本当に異常である割合)が悪くなることがあります。「偽陰性率」を優先するのか、「精度」を優先するのか、どちらもバランスよく必要なのか、で構築される数理モデルが異なります。通常、異常検知の場合には「偽陰性率」を優先する場合が多いようです。
ちなみに、偽陰性率ではなく以下の再現率(Recall)で考えることも多いです。
再現率 = 1-偽陰性率
再現率と精度の両方をバランスよく必要な場合、2つの指標の調和平均(逆数の和の逆数の2倍)であるF値を最適化する数理モデルの構築を目指します。