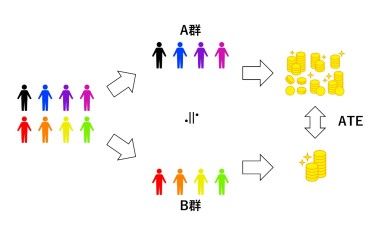
ABテストとは、例えばユーザをA群(処置群)とB群(統制群)に分け、どちらのほうが好成績を納めるのかをデータで確かめたりするアプローチです。
- A群(処置群):販促を受けた状態
- B群(統制群):通常の状態(販促を受けていない状態)
上の例ですと、A群の方がB群に比べ、有意に売上が高ければ、販促に効果があったと解釈できます。ABテストの理想の状態は、ある販促を受けたかどうか以外は、ほぼ同等の状況であることが好ましいです。しかし、色々な販促やキャンペーンが入り混じった、複雑な環境でABテストを実施することがあります。
例えば、A群やB群の中に別の販促を受けた状態の人もいるかもしれません。同じ部署の販促であれば、そのような状態にならないようにコントロールできるかもしれませんが、現実はそう簡単ではありません。
アプリの部署と、デジタル広告の部署、店頭販促の部署、サイト運営の部署、メール主体のCRMの部署など、各々バラバラに販促やキャンペーンを実施していたりしていなかったりします。さらに、そこに別の要因が絡み合ったりと複雑です。
そういった状況を打破するアプローチの1つとして、統計的因果推論の反実仮想アプローチがあります。今回は、「ABテストの代わりになりうる統計的因果推論の反実仮想アプローチ」というお話しをします。
【この連載の前回:シンプルで始めやすいABテスト入門 データ分析講座(その299) へのリンク】
1. 反実仮想(Counterfactual)
あるファストフードで、ある販促が効果があるかどうかを検証するため、メルマガ会員に対しABテストを実施することになりました。この販促に効果があるかどうかを確かめるには、次のような2つの状況を想定する必要があります。
- 状況A:メールを受け取った状態(販促を受けた状態)
- 状況B:メールを受け取ってない状態(販促を受けていない状態)
販促効果は、同じ人の状況Aの結果(購入金額)と状況Bの結果(購入金額)の差分から分かります。しかし、残念なことに、同じ人が状況Aと状況Bの2つの状態になることはありません。実現するのは、どちらか一方のみです。ある1人の人にとって、起こり得る事実は、状況Aか状況Bのどちらか1つです。起こらなかった事実を、事実に反しているということで、反実仮想と言います。例えば、サイトウさんがメールを受け取ったなら状況Aです。その場合、サイトウさんは状況Bになることはありません。サイトウさんにとって状況Aは事実で、状況Bは反実仮想です。
2. ABテストで解決
先程、販促効果は「同じ人の状況Aの結果(購入金額)と状況Bの結果(購入金額)の差分から分かります」と言いました。「同じ人」が、状況Aと状況Bの2つの状況になることはないので、このアプローチでは販促効果は分かりません。そこで、「同じ人」を「同じような人たち」という感じで、個から群(グループ)にします。
どう言うことかというと、販促効果は「同じような人たちの状況Aの結果(購入金額)と状況Bの結果(購入金額)の差分から考える」ということです。この差分を、平均処置効果(ATE、Average Treatment Effect)と言います。
そのためには、A群(状況Aになる人)とB群(状...
綺麗にランダムに割り付けられたかどうかは、色々な変数(データ項目)で、A群とB群それぞれで基礎統計量(平均値や分散など)や集計(単純集計やクロス集計など)、分布(ヒストグラムなど)などの結果を眺めてみることで確認できます。
3. 現実は厄介
現実は厄介です。そもそもランダムにA群とB群に分けていないケースもあります。販促を実施するとき、ある条件に一致した人のみ実施するケースです。そこに他のキャンペーンや販促がなされたりもします。さらにユーザの意思でA群かB群のどちらかに属するか決まることもあります。要は、理想的なABテストを実施することはなかなか困難ということです。色々な理由があると思いますが、機会損失がほぼ確実に生まれる、というビジネス的な理由が大きい気がします。
そこで機械学習で予測モデルを構築し、数理モデル上でA群とB群の状況を作り出し比較する、ということが考えられます。
4. 説明変数と目的変数
ある時点 (カットオフポイント) を選択し、その瞬間より前に起こったこと(原因)が、その瞬間以降に起こったこと (結果) を引き起こしたと仮定します。
- 処置変数(説明変数として利用):カットオフポイントより前に起こったこと(原因)
- 結果変数(目的変数として利用):カットオフポイント以降に起こったこと (結果)
処置変数は0-1の2値データです。予測モデルの説明変数になります。さらに、説明変数にデータに登場する各個人の属性項目(性年代、ライフステージなど)も利用します。共変量と呼ばれることが多いです。
先程、「販促を実施するとき、ある条件に一致した人のみ実施するケース」というお話しをしました。例えば、学生向けに実施した販促の場合、その年齢に相当する人がA群(販促を受けた人)になり、その状態でA群とB群を比較した結果は、使いものにはなりません。そうならないためにも、共変量をしっかり説明変数に組み込むことが求められます。
5. 処置変数をいじって効果と機会損失を測定
結果変数を目的変数に設定し、処置変数と共変量を説明変数に設定した予測モデルを機械学習で構築します。
そうすると、説明変数をいじることで、擬似的に2つの状況を作ることができます。
- 状況A:メールを受け取った状態(販促を受けた状態)
- 状況B:メールを受け取ってない状態(販促を受けていない状態)
この差分から、販促効果を見積もることができます。これを群別に実施することもあります。例えば、A群で実施した場合、それは販促のダイレクトな効果測定そのものになり、処置群における平均処置効果(ATT、Average Treatment effect on the Treated)と呼ばれます。コストデータを使い費用対効果などを計算し、効果の良し悪し検討に活用できます。
例えば、B群で実施した場合、それはB群に対する機会損失測定になり、統制群における平均処置効果(ATU、Average Treatment effect on the Untreated)と呼ばれます。今後、販促活動をB群へ拡大すべきかどうかの検討などに活用できます。
6. 傾向スコアで効果と機会損失を測定
A群とB群の割り当てがランダムではなく共変量に大きく依存するとき、共変量を使いA群 or B群を予測することができます。次のような分類問題を作ることができます。
- 目的変数:群(A群 or B群)
- 説明変数:共変量
この分類問題から、A群に属する確率(もしくは、B群に属する確率)が計算されます。
この確率は、その群に「割り当てされやすさ」を表す数値です。言い方を変えると、「らしさ」を表現する数値です。例えば、ある人のA群に属する確率が92%であれば、「A群らしい人」と言えるでしょう。一方、A群に属する確率が3%であれば、「A群らしくない人」と言えるでしょう。この「らしさ」を表す数値を、「傾向スコア」と言います。この傾向スコアの逆数を重みとして、平均処置効果(ATE、Average Treatment Effect)などを計算し、効果測定や機会損失の測定などを実施することができます。なぜならば、傾向スコアを用いたこのような調整により、A群とB群の共変量が同質に近づくからです。
例えば、A群で考えてみます。A群の中には、少数派ながらA群らしくない人がいます。傾向スコアの逆数を重みするということは、A群らしい人のデータの重みを小さくし、A群らしくない人のデータの重みを大きくすることです。
そうすることで、A群らしさを減退させ、通常のランダムアサイメントの状況に近づけます。
次回に続きます。