
1. XRDの相対強度
XRDにおいて回折パターンの相対強度におよぼす影響は、次の6項目があります。
- 構造因子
- 多重度因子
- かたより因子(偏光因子)
- Lorentz因子
- 吸収因子
- 温度因子
これら因子をまとめると次の式(1)が得られます。
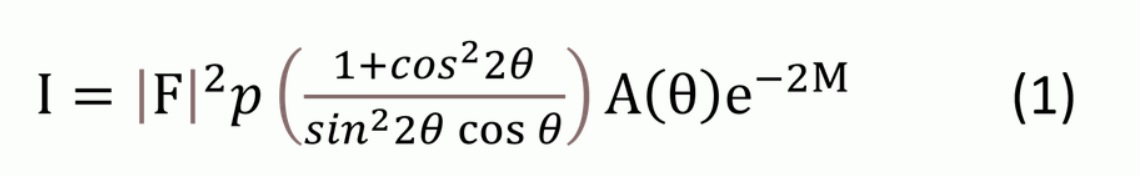
- I=相対積分強度
- F=構造因子
- p=多重度因子
- (1+cos22θ/sin22θcosθ)=Lorentz かたより因子
- A(θ)=吸収因子
- e-2M=温度因子
また、吸収因子と温度因子は省略されることもあるため、次の式(2)を使用することがあります。
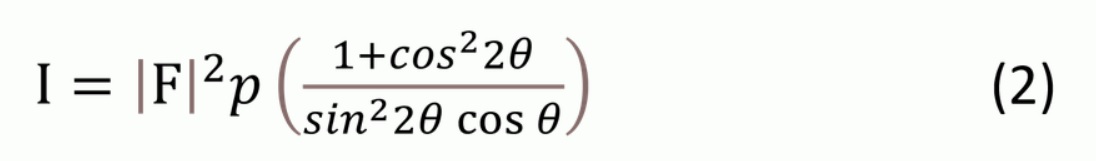
2. 構造因子
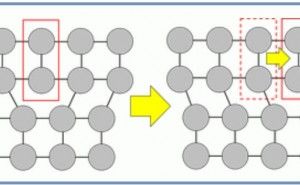
ブラッグの式に従って回折条件が起こるためには結晶構造を考慮する必要があります。
ブラッグの式dにおける結晶面の間隔は金属の格子定数ではなく、結晶構造のミラー指数(100)、(110)などの面間隔になります。しかし例えば体心立方格子と面心立方格子では(100)、(110)面などの原子配列は異なるため、回折を起こすミラー指数が異なります。そのため、各結晶構造で回折を起こすミラー指数を求める必要があります。これを構造因子として次の式(1)で表します。
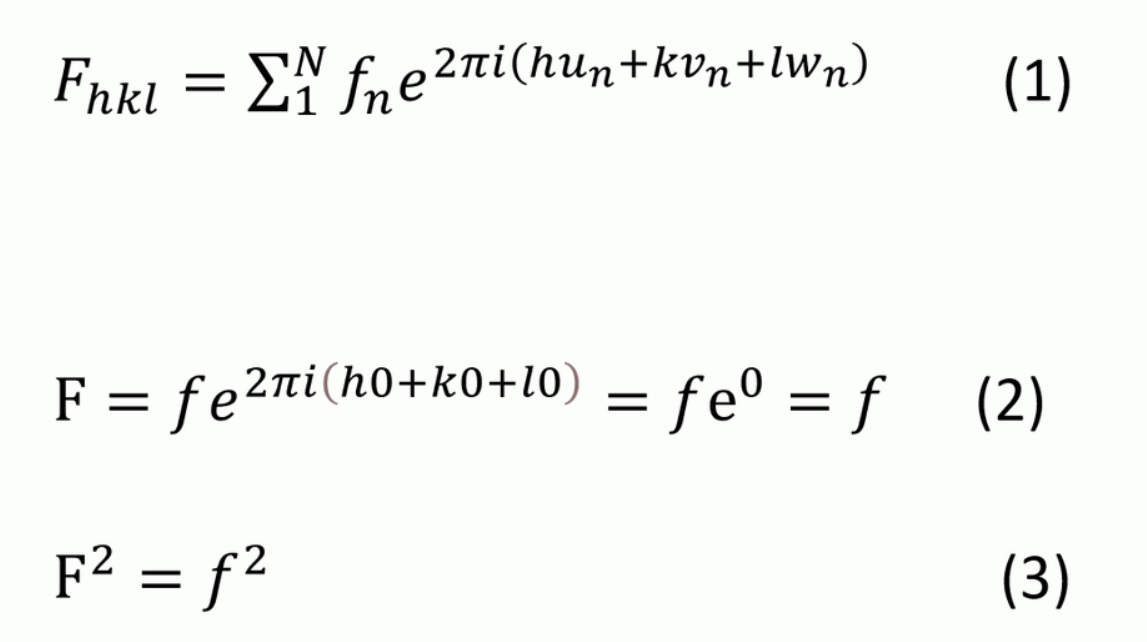
- F:構造因子
- f:原子散乱因子
- h、k、l:ミラー指数
- u、v、w:原子の座標
- n:各結晶構造で考慮する原子の数
構造因子を詳しく見ていきます。
例えば結晶構造が単純な立方晶の場合、立方晶の8個の頂点に原子が一つ配置した構造となります。そして基準となる原子1個に注目すると、この時の座標uvwは000となります。そして格子定数aの距離をu、v、wどの方向に移動しても、同じように原子が配列しています。このような原子の周期性を構造因子では000と表します。そして構造因子を計算すると上記の式(2)、(3)のようになります。なおe0=1です。
構造因子は2乗して回折ビーム強度を求めます。単純な立方晶では回折とミラー指数は無関係になり、どの面でも回折が起こるようになります。しかし構造因子が0になると原子の回折が打ち消し合うため、回折パターンは現れません。
次回に続きます。






















![金属材料基礎講座[機能材料・強度設計コース] 金属材料基礎講座[機能材料・強度設計コース]](https://assets.monodukuri.com/product/photo/5a73d3e9-bfc0-4c45-a6ba-2fc4e284732d.jpeg?d=0x0)







