一昔前とは異なり昨今の工業製品は構成が複雑化しており、性能を向上させるのに2つや3つの因子を修正しただけでは目標が達成できなくなっています。高度な製品の機能には100個以上の因子が影響していることも珍しくありません。
一方世の中はますます開発期間の短縮を要求してきており、実験の計画にあたっては出来るだけ多くの因子を出来るだけ少ないサンプル数で評価するという矛盾した条件が求められます。因子数が多い場合に、まともに多元配置実験を実行すると、気が遠くなるようなサンプル数を作ることになって現実的ではありません。そんな時には「直交表」を使うと効率的です。直交表を用いた工業実験の計画は主に日本で発展した方法で、日本の工業製品の優秀さの一つの理由は直交表であるとも言われるくらいです。
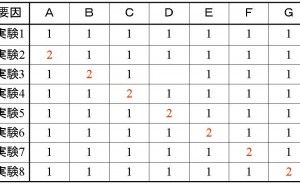
下の表1は、7つの因子A~Gに対して2水準の差を評価するときに使われる水準組合せの例で、「逐次実験」と呼ばれます。全ての因子を第1水準に取った実験(サンプル)1に対して、実験2~8で一つずつ因子の水準を変えることで、因子の効果を見ます。
表1.逐次実験組み合わせ
一方次の表2は同じ実験で直交表L8を使った時の水準組合せになります。8通りのサンプルで組合せを変え、実験1が全て第1水準である点は同じですが、実験全体では水準1と2がある法則に従い同数ずつ配置されています。
この組合せがミソで、各要因ごとに二つの水準が4回ずつというだけでなく、ある要因の一方の水準に対して残りの全ての要因の両水準は2回ずつ平等に入っています。これを各要因が「直交している」と呼び、直交表の名前に繋がります。
これによってたった8回の実験で7つの要因がそれぞれ繰り返し数4という信頼性の高い実験が可能となります。表1の逐次実験は各要因の繰り返し数1ですから、実験効率が4倍になったということもできます。
表2.L8直交表組み合わせ
直交表はなぜそんな魔法のようなことができるのでしょう?
多元配置実験で実験数が掛け算で増える理由は、3つの要因を評価する3元配置なら3次、5元配置なら5次までの交互作用をすべて評価するからです。ややこしい話ですが、たとえばA、B、C、D、E、Fという5つの要因を2水準で評価するに当たり、A1、B1、C1、D1の時とA1、B2、C1、D2の時の因子Eの効果の違いまで考えるということなのです。高次の交互作用が有意である可能性はありますが、E因子の主効果に比べれば極めて小さいはずですし、その意味を解釈することは極めて難しいことが想定されます。またそのように複雑な交互作用の上に成り立つ条件は、環境など他の因子に対しても非常に不安定なことが一般的です。
5つの因子の主効果だけを2水準で評価するのには、理論的に6回の実験で済むはずですが、残念ながら2水準系で5因子の直交表は提案されていないので、8回の実験で7因子を評価するL8という直交表の5列に因子を割り付け、余った2列は交互作用を評価するか、誤差列として検定力を上げるのに使うことになります。実践的には、たとえ交互作用がないと予想されても...
直交表の種類を示すのにLが使われるのは、ラテン方格(Latin Square)を発展させたモデルだからです。
品質工学をやさしく解説するセミナーDVD好評発売中!
「品質問題の未然防止は難しくない!-品質工学の基本的な考え方-」
http://www.monodukuri.com/dvd_library/dt/6