実際の実験ではサンプルの損傷や仕様違いのサンプル作成等により、どうしても欠測値が発生します。そこで実験の精度、信頼性を上げるために同一条件のサンプルを2つ以上作成する場合がよくあります。もしサンプル作成を1つ失敗してももう1つでデータが取れますし、2つとも作成できた時は平均値を取ることで信頼性が向上すると考えられます。
しかし考えてみるとn=2でサンプル数が2倍になった割りには、得られる結果はさほど変わらず、何よりもし同一条件の2サンプルが失敗すると全く評価できません。サンプル損傷でも仕様違いにしても同一条件のサンプルは一緒に作成することが多いので、こういったケースも珍しくないのではないでしょうか?
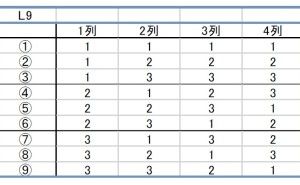
それでは、直交表を使った場合はどうでしょう。もともと直交表では各因子の水準は同数回出現するため、例えばL8で1サンプルが損傷して因子A第1水準のデータがひとつ取れなくなっても、他の7サンプルに第1水準がまだ3サンプル残ります。他の因子についても同様で、直交関係は崩れるものの壊滅的な結果にはなりません。
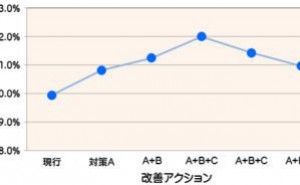
そんな時の処理方法としては、「逐次近似法」が取られます。すなわち第0次近似として作成した7サンプルの測定平均値を欠測サンプルのデータとして要因効果図を求め、ここから欠測値を推定し、その値を第1次近似値としてもう一度解析して要因効果図を求める。これをデータが収束するまで繰り返すものです。
予想されるように、サイズの大きい直交表を使っている時ほど早く収束し、L18ですと0次近似でも充分使える結果を示すほどです。 n=2と比べた利点は、よほど多数のサンプルが偏って欠測値にならない限り(例えばL18で5個欠測し、すべて6個あるC因子の第1水準だったとか)補正が可能という点と、作成したサンプルすべてが実験信頼性向上に均等に貢献している事です。
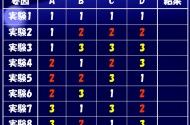
下表1は従来の典型的な繰り返し数2の実験で、4因子を2水準で評価するのに10サンプル使っていますが、最悪2サンプル(例えばNo.7と8)作成に失敗すると、ある因子の評価が全く出来なくなります。
表1.4因子の繰り返し2回実験
| 実験No. | 要因A | 要因B | 要因C | 要因D |
| 1 | 標準 | 標準 | 標準 | 標準 |
| 2 | 標準 | 標準 | 標準 | 標準 |
| 3 | 水準A2 | 標準 | 標準 | 標準 |
| 4 | 水準A2 | 標準 | 標準 | 標準 |
| 5 | 標準 | 水準B2 | 標準 | 標準 |
| 6 | 標準 | 水準B2 | 標準 | 標準 |
| 7 | 標準 | 標準 | 水準C2 | 標準 |
| 8 | 標準 | 標準 | 水準C2 | 標準 |
| 9 | 標準 | 標準 | 標準 | 水準D2 |
| 10 | 標準 | 標準 | 標準 | 水準D2 |
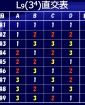
下表2は直交表L8を使って同様の実験を組んだ例で、8サンプルで7因子を2水準で評価可能であり、例えば2サンプルの作成に失敗するとその影響はすべての因子に及びますが、逐次近似法を取ることで評価が不能となる因子は発生しません。
表2. 7因子L8直交表実験
| 実験No. | 要因A | 要因B | 要因C | 要因D | 要因E | 要因F | 要因G |
| 1 | 標準 | 標準 | 標準 | 標準 | 標準 | 標準 | 標準 |
| 2 | 標準 | 標準 | 標準 | 水準D2 | 水準E2 | 水準F2 | 水準G2 |
| 3 | 標準 | 水準B... |