SQC(Statistical Quality Control:統計的品質管理)というと、期待値、確率変数、標準偏差、正規分布、共分散、公差、確率分布などの言葉と、QC七つ道具、実験計画法、回帰分析、多変量解析などの統計的方法や抜取検査、サンプリングなどの手法が出てきます。統計的品質管理はSQCの言葉を理解して最適な手法を駆使した品質管理です。 戦後の日本製造業を強くしたのは、デミング博士がこれらを持ち込み、教育指導したためです。経験や勘に頼るのではなく、事実とデータに基づいた管理を重視する点が特徴です。
今回は、最初に偏差と分散を整理して解説した後に、分散の加法性について解説します。
◆ばらつきの算出~偏差と分散
統計学を学び始めると最初に出てくるのが標本と母集団や「ばらつき」の説明です。まず始めに「ばらつき」とは一般的にどう言う意味でしょうか。広辞苑では次のように解説してありました。 「測定した数値などが平均値や標準値の前後に不規則に分布すること。また、ふぞろいの程度。」
統計でばらつきと言えば直ぐに思い浮かべるのは「標準偏差」だと思います。ばらつきを表す統計量である標準偏差は最もポピュラーな統計量の一つです。 エクセルを使えば面倒な計算式を入れずとも一発でドーンと算出できます。
標準偏差の算出、個人的には統計を数学的に考え過ぎると食わず嫌いになってしまうので数学のように式の展開過程を深追いするのはお勧めしません。Σの記号が出てくるともう見たくないって気持ちになりませんか、ただ標準偏差の計算式を導く過程は逆にばらつきの定義の理解を深める事に役立つので紹介します。
1. 偏差と分散
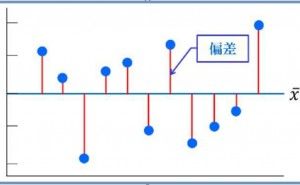
標準偏差=分散の平方根です。偏差は分散の計算に用いられるからです。偏差は平均値と各データの差です。 図1が、イメージです。
Xの上に横棒を引いた記号はデータXの平均値を表します。例えば平均値50点の試験結果で56点の人の偏差は6点です。47点の人の偏差は-3点です。わかりやすいですね。偏差を合計すればばらつきの程度が分かるような気がしませんか。でも平均値からのプラスとマイナスを足すわけなので全部足したら”ゼロ”になります。そこでゼロに成らないように各偏差を自乗して和を取ります。この”偏差の自乗和が偏差平方和“です。 エクセル関数はdevsqです。データを選べば勝手に平均を算出し各データとの偏差を算出し自乗和を返します。
次にこの偏差平方和をデータ数で割ったものが”分散“です。例えば10個のデータの偏差平方和を計算しそれを10で割れば分散が算出出来ます。ただし正確には”母分散“です。
母集団の偏差を導きたい場合は分散は全データ数Nで割ることで算出されますが一部の データn個をサンプルとして抜き取りそのデータから母分散値を推定する場合はn-1で 割ります。何故サンプルデータから計算する場合はn-1になるのかの説明は一端置いといて一部の データからばらつきを求めた場合は全てのデータから求めた場合よりも小さくなると思 いませんか。
サンプルデータは当然母集団全てのデータより少ないので滅多に出現しない平均値から 離れたデータが含まれる可能性も低いです。平均値に近いデータだけで計算すると全データでの計算値よりも小さくなってしまうの でサンプルだけで母集団の分散を推定する場合は補正が必要なのです。よってデータ1つ分小さい数値n-1で割ってやるのだと理解してみて下さい。ちなみにn-1は自由度と呼ばれています。
今度は数学的に説明すると偏差の和はゼロになると上で述べました。「各データと平均値の差(=偏差)」の和がゼロの数式が成り立ちます。未知数Xが5個あってもこの数式を用いれば4つ分かれば残り一つは決まります。つまりn個の未知数があればn-1個が分かれば残り一つは自動的に決まります。分かりやすく言えばn-1人は自由に椅子を選べるが残りの人は自ずと残った椅子に座ら ざるを得ないと言う感じです。その為自由度と呼ぶと思って下さい。分散が出たら後はその平方根を計算すれば標準偏差となります。 平方根を取るのはデータを自乗しているので元の単位に戻すためです。
言葉だとわかりにくいかもしれませんが上図と合わせてイメージは掴めると思います。細かい事ですが母集団全てのデータが使える場合は全データ数で割り、サンプルで母集団の分散を推測する場合はデータ数-1で割るという事を覚えて下さい。分散は他の統計的手法でも度々出てきますので是非理解を深めて下さい。
◆ 分散の加法性 ばらつきの合計