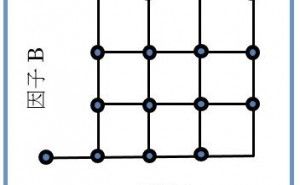
昔の事になりますが、配属された職場の先輩の下である実験を手伝いました。先輩は図1のような計画をたてました。2つの量的因子A、Bの効果を確認する実験でした。
図1.2因子15実験（アンバランスな配置）
ここでのポイントは、次の3つです。非線形性を評価するために各因子は4水準、一方の因子が最小値のとき他方の因子の最大値は調べない。両因子が最小値のとき、因子Aだけ水準を1つ下げて追加評価、先輩は少ない実験回数で「あれこれ」調べるため、あえてアンバランスな実験を計画しましたが、「信頼できる結果」を得る確信があったでしょうか。結局1ヶ月後の報告会で先輩は「いろいろやったのですが、よくわかりませんでした」と報告しました。このとき私が得た教訓は「信頼できる結果を確実に得るには統計的手法を活用すること」でした。その1つが実験計画法です。
それから、この手法を活用して多くの実験を行ってきました。計画段階では信頼できる結果を確実に得るための保守性が1つのポイントです。もし前記の先輩の実験を修正するならば、図2の二元配置が基本となります。なぜなら2因子4水準の水準組合せを確実に評価するなら、バランスのとれた実験が望ましいからです。さらに不測の事態で欠測値が生じた場合でも、この計画ならその欠けた値を推定して解析を続けることも可能です。もちろんこれは非常に保守的ですが、しかし確実な報告が求められていた当時の状況を考えると、この計画が必要にして十分であったのです。
図2.2因子16実験（二元配置）
そして、もし今、私が独自に計画するならば、3因子が評価できる図3の中心複合計画を検討するでしょう。これは立方体の8頂点と重心点さらに6面の中心点の延長上を実験点として非線型性を評価するもので、応答曲面法と呼...
ばれる手法の1つです。さらに実験点を少なくするのなら、最適計画（Optimum Experimental Design）を利用するかもしれません。
図3.3因子15実験（中心複合計画）
この文書は、 2016年4月21日の日刊工業新聞掲載記事を筆者により改変したものです。