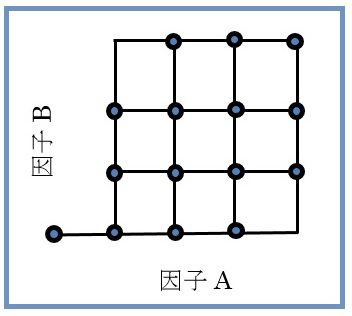
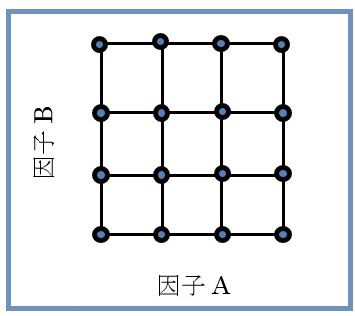
昔の事になりますが、配属された職場の先輩の下である実験を手伝いました。先輩は図1のような計画をたてました。2つの量的因子A、Bの効果を確認する実験でした。
TOP

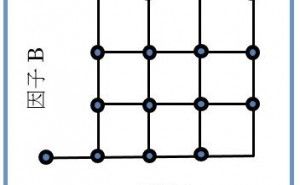
昔の事になりますが、配属された職場の先輩の下である実験を手伝いました。先輩は図1のような計画をたてました。2つの量的因子A、Bの効果を確認する実験でした。


昔の事になりますが、配属された職場の先輩の下である実験を手伝いました。先輩は図1のような計画をたてました。2つの量的因子A、Bの効果を確認する実験でした。


続きを読むには・・・
小川 昭
統計とITの活用で現場の暗黙知を可視化し、問題解決やプロジェクトの課題達成をする総合的品質経営(TQM)のスペシャリスト!
統計とITの活用で現場の暗黙知を可視化し、問題解決やプロジェクトの課題達成をする総合的品質経営(TQM)のスペシャリスト!
【層別因子を含むデータ解析 連載目次】 重回帰分析初心者向けの注意 ~ 水準2個の場合 重回帰分析初心者向けの注意 ~ 水準3...
【層別因子を含むデータ解析 連載目次】 重回帰分析初心者向けの注意 ~ 水準2個の場合 重回帰分析初心者向けの注意 ~ 水準3...
1. 天体運動に思い馳せたピタゴラス 数学といえば、現場数学であろうが純粋数学であろうが、何と言ってもピタゴラスです。紀元前500...
1. 天体運動に思い馳せたピタゴラス 数学といえば、現場数学であろうが純粋数学であろうが、何と言ってもピタゴラスです。紀元前500...
♦ 日本文化伝承する規矩準縄術 1.曲尺と発音 棟梁(とうりょう)をはじめとする大工さんたちの腕の素晴らしさは、日本...
♦ 日本文化伝承する規矩準縄術 1.曲尺と発音 棟梁(とうりょう)をはじめとする大工さんたちの腕の素晴らしさは、日本...
DPMOとはDefects Per Million Opportunityのイニシャルを取ったものです。DPMOを百万個当りの欠陥数(製品百万個当りの不...
DPMOとはDefects Per Million Opportunityのイニシャルを取ったものです。DPMOを百万個当りの欠陥数(製品百万個当りの不...
ビックデータ時代を考える事例として、今回の第45代米国大統領選挙を見てみます。第45代の米国大統領に、ドナルド・トランプ氏が決まりましたが、トランプ氏当...
ビックデータ時代を考える事例として、今回の第45代米国大統領選挙を見てみます。第45代の米国大統領に、ドナルド・トランプ氏が決まりましたが、トランプ氏当...
ボーイング 737 Max 8機が短い期間に2回の墜落死亡事故を起こし、多くの航空会社が同機種の運航を停止する事態となっています。多くの...
ボーイング 737 Max 8機が短い期間に2回の墜落死亡事故を起こし、多くの航空会社が同機種の運航を停止する事態となっています。多くの...
© ものづくりドットコム / ㈱産業革新研究所
ものづくりドットコムのIDでログイン

まだ未登録の方は、「無料」会員登録で多くの特典が!
Aperza IDでログイン
Aperza IDでのログイン機能は終了いたしました。
今後はものづくりドットコム会員ご登録の上、ログインをお願いいたします





