【層別因子を含むデータ解析 連載目次】
♦ 重回帰分析初心者向けの注意 ~ 水準3個以上の場合
前回の本解説記事(その1)では、層別因子の水準が2個(機械号機が2台とか男女差とかなど…)の場合は、割り当てる数値を何に例えてもよいことを確認しました。今回は、この水準数が3個以上の場合についてお話します。結論を先にいえば、2個の場合と違い、きちんとした定義変数を割り当てる必要があります。機械号機の1号機、2号機、3号機に適当に、―1、0、1とか、1、2、3とかを割り当てることは厳禁ということです。2水準の時には、結局、大小を区別するというよりは、一応区別するが、号機はそのどちらでもいいわけです。例えば、号機別に1個ずつのデータを取ったとしましょう。号機に1や2を割り当てて、その散布図を想像しましょう。その方程式は直線にしかなりません。どんな適当な数値を割り当てても、直線にしかなりません。傾きは、変わりますが回帰するなら、定義した割り当てた数字を入れればいいので、yはそれに対応して出てきますから、同じことです。データ数が増えてもばらつき具合は、回帰線の中心(平均値)に一致するだけで、状況は変わりません。
機械号機差や材料メーカー差、成長炉差、支店の差などで2水準で比べるなら、どんな数値を当てがってもよいですが、3水準以上ではダメです。一番簡単な理解は、号機に1、2、3を割り当てて、収率が10%、40%、70%とする場合を思い浮かべてください(下記表1.参照)。
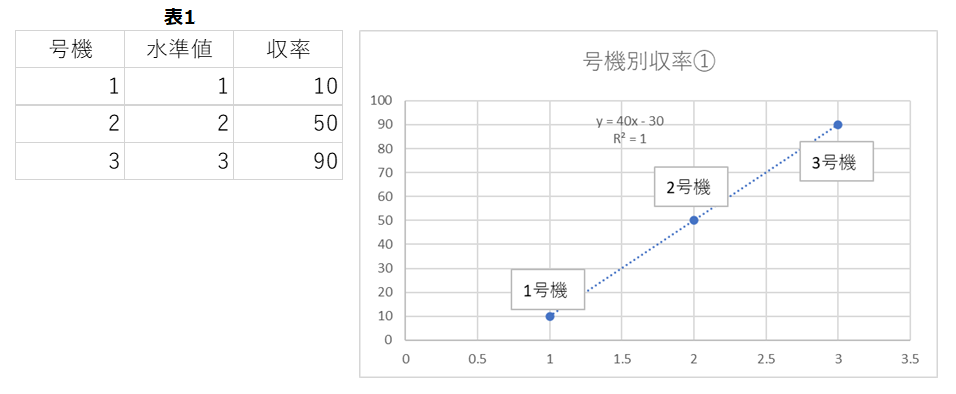
図1.水準値と号機と収率グラフ①
次に、水準値を逆にしてみます(表2参照)。
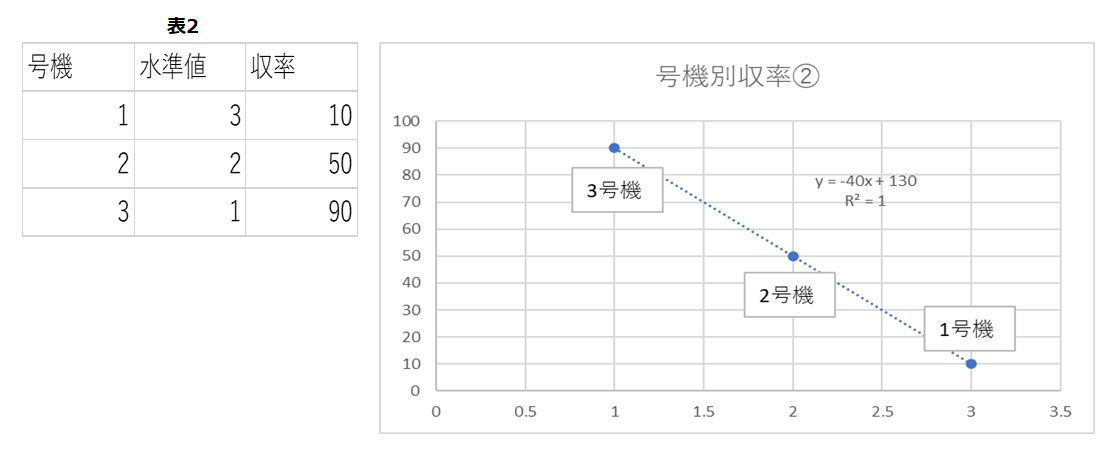
図2.水準値と号機と収率グラフ②
回帰式は違いますが、特にここまでなら実害はありません。順序に注意するだけです。ところが、このやり方は非常に重要な誤りを誘導します。それは知らずと、号機の順序を決めているので、2水準の時のようなら、どう入れ替えても、大小が変わるだけですが(表1、2、図1、2参照)、今回の2号機はここまで、常に真ん中にあったわけです。1、2、3あるいは3、2、1という水準値の与え方は2号機が必ず、1号機と3号機の中間にあるという定義になってしまっているわけです。これはおかしな話です。1号、2号といってもA、Bとか太郎、花子というネーミングに過ぎないので、大小順列関係を考えた水準はおかしなことになります。実際にやってみましょう。
下記表では、2号機を端に配置した水準値としています。
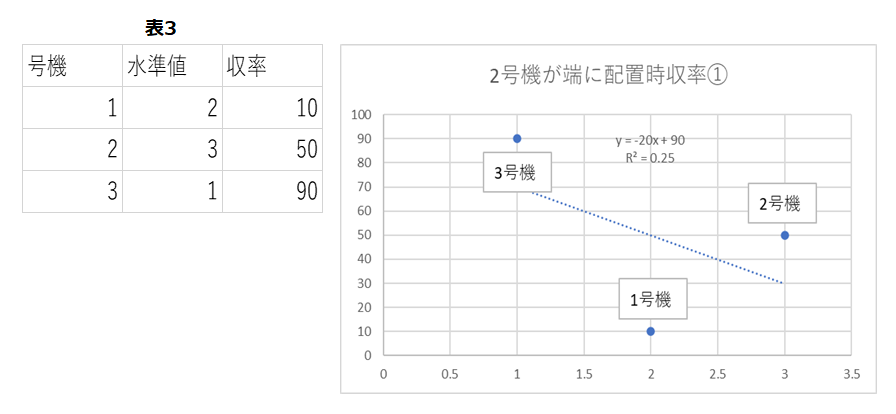
図3.2号機を端水準にした場合
回帰式は役に立ちそうにありません。決定係数も25%となります。同じ事象を見ているのに、収率と号機の関係はほとんどないこととなります。差があるともいえないが、差がないともいえないということです。検定が必要になりますが、ここでは行いません。
以上を単回帰で説明してきましたが、そろそろ重回帰に戻して説明します。今までのまとめは、
- 2水準なら適当に数値を入れればよい
- 3水準以上は、適当にいれると、数値が順序(大小)を表すことになり、厳禁
そこで、どうするかです
例えば、説明変数x1とx2は計量因子(温度とか圧力のような連続計量値)とし、号機が4個(A1、A2、A3、A4)とした場合、下表のように置き換えます。これを定義変数といいます。
表4. 号機が4個の場合の定義変数
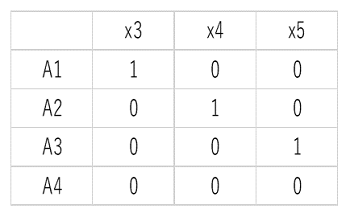
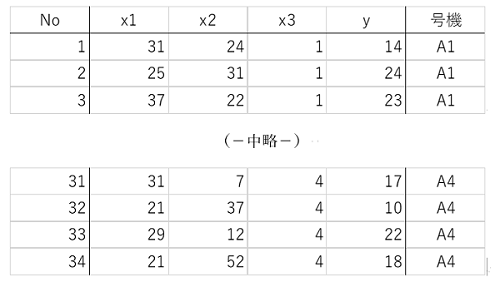
生データは前回解説記事の表2を使って、以下のようになります。
表5. 号機別の連データ
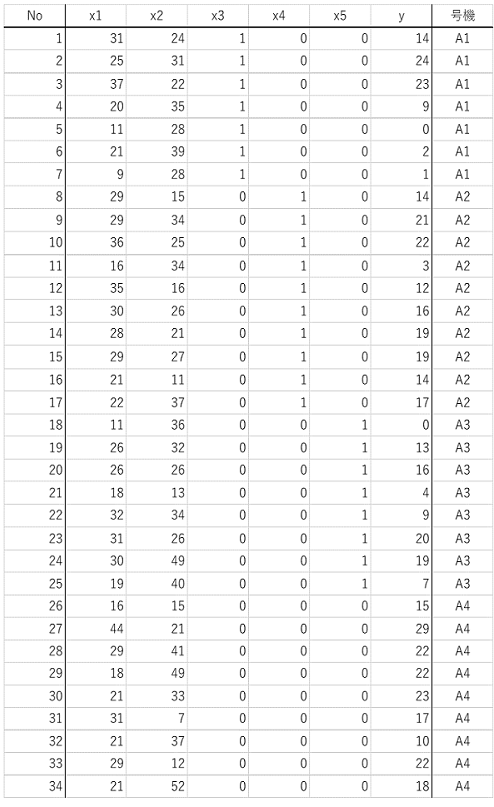
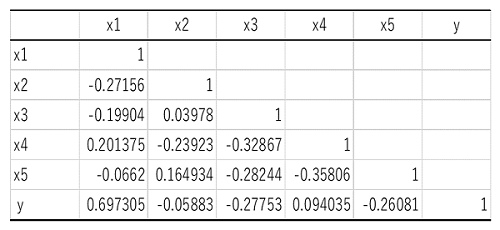
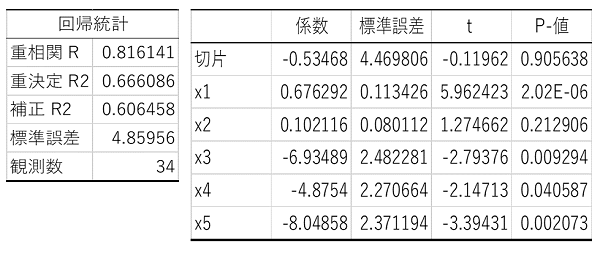
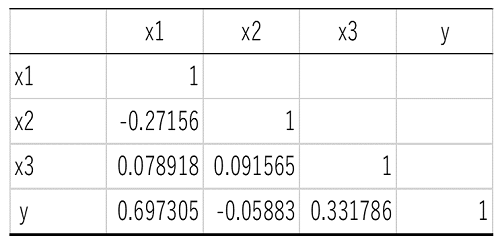
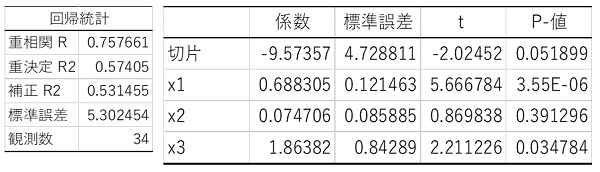
相関行列や重回帰分析の結果は以下の...