1. 天体運動に思い馳せたピタゴラス
数学といえば、現場数学であろうが純粋数学であろうが、何と言ってもピタゴラスです。紀元前500年位に、既に直角三角形の斜辺の長さの自乗は、残りの2辺の長さの自乗の和に等しいというピタゴラスの定理を発見している本当の天才なのです。ピタゴラスは、今の数学の基礎どころか、地球を含む天体が球体であることを見破っていました。コペルニクスの地動説は、ピタゴラスの先見の明によると言っても過言ではありません。観測機材などほとんどなかった時代に、どうやって天体の運動にまで思いを巡らせたのでしょうか?ピタゴラスは、教団の主催者であり、魂の解放のための儀式を行ったりしていて、現在の科学者とは全く異なります。彼は、素数や平方数に興味を持ち、宇宙の秩序や調和をもたらす源泉としての「数」に関する思考を重ねたと思われます。
私はギターを弾きます。弦楽器は波動や音の勉強をするのに都合の良いものなので、教室でギターを弾いて生徒に教えます。「棹(さお)」(ネック)が胴の部分に繋がっているところで弦がちょうど半分の長さになり、開放弦から1オクターブ上の音が出ます。7フレットは3分の2で開放弦をドとすればソの音。5フレットは4分の3でファの音。波動の節の部分なので、ちゃんと弦を押さえなくとも、軽く弦に触れて振動を止めれば高調波を作れることが分かって、波動の理解を深めることが出来ます。3/2が1と2の相加平均(算術平均)で、4/3がそれらの調和平均であるところも奇跡的です。
2. 天体の間隔と「ピタゴラス音階」
さて、ドとミはどうでしょうか?これを5/4とするのが純正律です。ドミソの和音が4:5:6でぴったり合います。しかし、この方法では、半音は16/15なのですが、全音に9/8と10/9の2種類が出来てしまいます。そのため、純正律の楽器のキーにはド#とレ♭が別にありました。
ピタゴラスはピタゴラス音階と呼ばれる別のやり方をしました。それは、ドとソの関係(完全5度)を次々と適用するのです。ソの次がレで9/8、次がラで27/16、そしてミは81/64になります。しかし、純正調と同様に、ある音の振動数の比で他の音を設定する方法では、どの調に対しても完全な和音を作ることは不可能です。そこで、ピアノの調律は、半音が全て同じ比率で増えて行く(12√2=1.059...ずつ)平均律を使っています。完全に和音は合いませんが、調律によってその「合わなさ」が違うこともありません。適当に手を打った調律なのです。音楽の先生がピアノでドレミの和音を弾いて、それを金科玉条の様にきれいな和音であると教えるのはうそなのです!
ピタゴラスのレベルになると、こんなものではありません。想像たくましく、天体は和音を生み出す弦の長さに対応した間隔に並んでおり、その運行により音楽を奏でている、というのです。それを、彼は「天体の調和」と呼びました。
3. ケプラーの3法則から万有引力へ
16世紀に入り、ケプラーが惑星の運動を記述できる3法則を発見しました。しかし、彼は科学者とはいっても、ピタゴラスを信奉し、天体は音楽を奏でると信じていたようです。彼は、占星術師でもありました。
ニュートンの偉いところは、旧来からの思い込みを廃し、万有引力という概念を打ち立てたことです。彼の理論はケプラーの法則が成り立つ様に作られました。重力のポテンシャルが1/rであるというのは、力が1/r2だからです。これは、力の源泉からの距離rのところの球面の面積が4πr2なので、力が減衰せずに広がっていくとすれば、その保存則として必須の式になります。つまり、重力や電磁気力の1/rのポテンシャルは、3次元空間の一様性を表しているのです。
明るさはルックスで表されますが、これも光源の光度であるカンデラから1/r2で減少することは3次元空間に一様に広がるからです。有名な話を挙げます。夜空の星が一様に分布しているとします。それが如何(いか)に薄い密度で分布しているとしても、自分から距離rのところには4πr2に比例した星があることになります。すると、1つの星からの光が1/r2で減りますが、rの距離にある厚さΔrの球面からの明るさへの寄与は一定になります。無限遠まで積分すると、
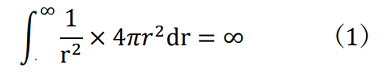
となり、発散するのです。これでは、夜はピカピカと輝いてしまいます。夜が暗いという事実から、以上の想定は成り立たず、結局、宇宙は膨張し、赤方変位をしながら我々から遠ざかっていなければならないことが分かったのです。
4. 月面の模様がいつも同じなのは奇跡的!?
月はいつもウサギが餅を突いている模様の見える側を地球に向けて地球の周りを回っている...