1. 誤差の概念について
子どもの頃、面積を求める問題は分かりやすく、誰でも算数が出来た気になりました。その時、悩みもせず、例えば、a=1.8mでb=2.7mなら、長方形の面積S= a×bだから、4.86㎡と答えました。もちろん「○」をもらったはずです。
これで良かったのでしょうか?実は、大学を卒業するまで、本当に誤差の概念は適当にしか教わって来ませんでしたし、理屈では分かっていても、定量的に確認したことがなかったのです。この問題、表示された長さの測定誤差を考えると(極端な話だといわれるかも知れませんが…)a=1.8±0.05m、つまり、a=1.7500…m~1.84999…mまでの範囲を意味している可能性があります。その理由は、そもそも誤差や有効桁数を表示していないからです。
bも同様で、2.65000…m~2.74999…mの範囲にある、と理解すべきなのです。すると、Sの最小値と最大値は、計算してみればすぐ分かりますが、3桁まで表示すれば、4.64㎡~5.09㎡の範囲にあることになります。こんなに違う?と驚かれるかも知れませんが、この通りなのです。そもそも長さの方に2桁の精度しかなかったので、4.86㎡という結果はそれを無視しており、4.9㎡と書くべきでした。
2つの数の演算を行う場合、加減算をするなら、誤差も線形にしか発生しません。長さの和の例であった場合なら、
そのまま計算して、
c=a+b=4.5m (1)
なのが、誤差を加味して計算すると
c=a+b=4.4m~4.6m (2)
となるだけです。
つまり、2つの長さを測ってその和を取ると誤差も足されるだけなのです。
ところが、掛け算の場合にはそうはいかないのです。
S=(a±Δa)×(b±Δb) (3)
なので、
S=a×b-a×Δb-b×Δa+Δa×Δb~a×b+a×Δb+b×Δa+Δa×Δb (4)
まで可能になります。つまり、ちょっとした誤差が掛け算によって拡大されることになるのです。
元の数値にあった誤差が最終結果に影響を与えることを誤差の伝播と呼びます。何となく、誤差というから小さい値であり、それは最終結果にも小さな影響しかない、と単純に思い込んでいることが多いのです。しかし、面積の例どころか、とんでもなく拡大して伝播することもあるので要注意な事項なのです。
複数の変数の多くの測定値の平均値として何らかの値を計算によって求める場合の一般的な誤差伝播はより複雑になります。室温で実験する場合の物理量には常に揺らぎがあり、この問題が発生します。変数x, y,…の関数として f が定義されている時、その値 F
F=f(x,y…) (5)
に対し、x, y, …に標準偏差σx、σx・・・がある場合、F の標準偏差σF の2乗(分散)は、
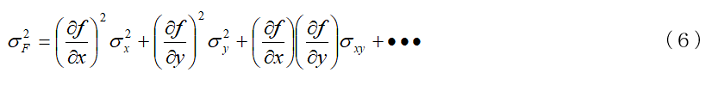
となります。共分散 は変数に相関がある場合に発生します。一番簡単な f が加減算の場合には、

であり、f が掛け算の場合には、
![]()
となります。
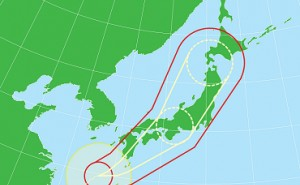
2. よく見掛ける誤差表示は台風進路の予報円
部品を組み合わせて自動車等の機械を作る場合、部品ごとに「まち」や「あそび」と呼ばれる余裕が持たされています。これは、最終製品を製作困難にせず、価格を抑えながら十分な精度を確保するための方策なのです。そのため、この許容誤差範囲は公差と呼ばれるのです。自然現象も人間の予測通りにはいきません。地震や台風の進路予測は、如何(いか)にスーパーコンピューターが高速になっても入力データが完璧ではなく、さらに計算プログラムが多くの近似を使うため実に困難です。良く見る誤差表示は、天気予報で台風の進路を示す時に描かれている丸い円です(その円さえ次...