【目次】
第5章 マトリックス・データ(MD)解析法の使い方←今回
第6章 マトリックス図法の使い方
第7章 系統図法の使い方
第8章 アロー・ダイヤグラム法の使い方
第5章 マトリックス・データ(MD)解析法の使い方
5.1 MD解析法について
5.1.3 多変量解析法ニーズの高まりの背景
ここで、MD解析法に対する理解を深める意味で、多変量解析法のニーズの高まりの背景について触れておきます。上記の定義にある通り、多変量解析法の解析対象は、「多種多様の特性からなる複雑な事象」です。
ならば、多変量解析法以外の解析対象は、「単一特性からなる単純な事象」ということになりますが、そのような事象が世の中に存在するのかという疑問が生じます。実際はそのような事象が存在するわけはなく、“本来多種多様な特性を持つ複雑な事象だが、ある単一特性の側面に絞って論じても差し支えない場合”か、“本来複雑な事象を、特性間の独立性を維持しつつ、単一特性として取り扱ってもよいところまでブレークダウンする要素還元法の適用が許される場合”かのどちらかです。
このようなとらえ方は、最近多変量解析法のニーズが高まっているのが、コンピューターの発達と普及だけではないことを知る上で大切です。というのは、社会が進化し複雑さを増した現在、取り扱うべき事象が、単一特性の側面に絞った取り組みでは意味をなさなかったり、要素還元法の大前提である“特性間の独立性を維持”してのブレークダウンが難しくなり、事象の持つ複雑さをそのまま受け入れる形での“総合的な取り組み”が必要になってきたことが、多変量解析法のニーズが高まってきている大きな理由といえます。
このことは、現在の社会問題に対する対応が、事象の単純化是認を前提にした“縦割り組織”が立ちはだかって遅々として進まない現状や、学問の世界における要素還元法を前提にした“縦割り組織”が、新たな学問分野(複雑系が好例)の出現に戸惑う状況を見るとき、より身近な問題として把握できるのではないでしょうか。
こういった現状を考えるとき、N7にMD解析法(主成分分析法)が含まれていることは、多変量解析法への橋頭堡として意義深く、納谷部会長の先見の明に改めて畏敬の念を禁じ得ないところです。(注)
(注)聞くところによると、QC手法開発部会がN7の開発に取り組んでおられた当時、納谷部会長が日科技連主催の関西多変量解析部会長も兼務しておられた関係で多変量解析手法を分かり易い形でのN7への採用が話題に上がり納谷部会長が主成分分析を取りあげ、馴染みやすい「マトリックス・データ解析法」と名付けて採用されたとのことです。
5.1.4 SQCにおけるMD解析法の位置づけ
MD解析法は、多変量解析の1つと聞いただけで難解で遠い存在との認識から、取り組む前に拒否反応を呈するのが普及を妨げているといえます。その例外ではなかった筆者を、その呪縛から解いてくれたのが、表5-1のような位置づけと把握です。
この表は、あるテーマに重回帰分析を活用した際、ふとしたことからMD解析法に思いが及んで行き着いたものですが、このような位置づけでMD解析法を把握したことにより、急激に身近に感じることができたのです。
というのは、数理統計学的に身近な手法の延長線上でとらえることにより親近感を覚えたのと、MD解析法の活用対象を“被説明変数を持たない”としたことにより、事例で紹介しますが、具体的な活用テーマを手に入れることができたのです。
表5-1 SQCにおけるMD解析法の位置づけ
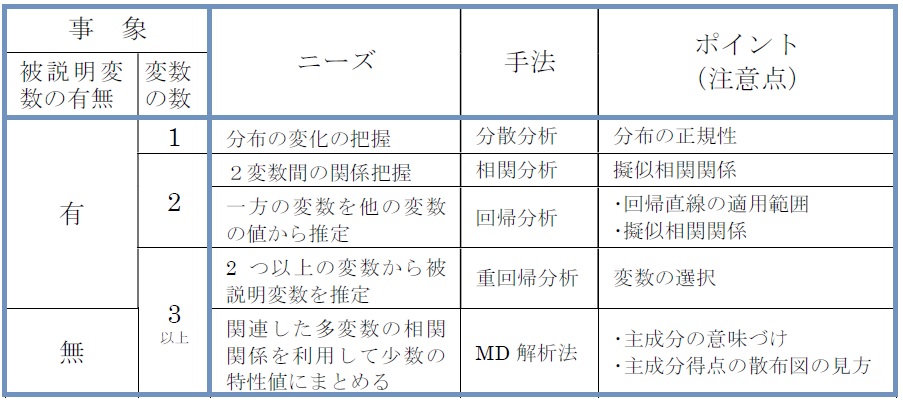
ところで、この私的な把握表を披露した背景には、上述したような建前的な流れとは別に「MD解析法の敬遠は、ある種の問題解決の放棄を意味することが、上表から明白であり、手法の難解さをうんぬんする次元の話ではない」という、スタッフとしてのプライドに迫る、一種せっぱ詰まった思いのあったことを伝え、共感を得たかったのです。
いま一つ、上表を得てよかったのは、解析対象事象の“被説明変数の有無”に着眼した点です。なぜなら、この“被説明変数の有無”が、我々にとって問題解決の難易度を決定づける要因だと思うからです。
というのは、被説明変数が存在する場合は、何をすればよいのかがある程度分かっており、実施したときの効果の把握が可能という、我々日本の産業人の最も得意とするところです。
ところが、被説明変数がない場合というのは、何をすればよいのかが漠然としていてつかみどころがない上、たとえ効果的と思われる策が見つかっても、実施結果の評価のしようがないという状況を意味するからです。
そして、こういった状況こそが、過去の延長線上にはない時代の趨勢であり、“21世紀型スタッフワーク”の重要なテーマなのだが、我々日本の産業人...



