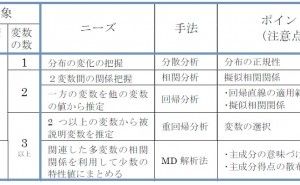
【目次】
第5章 マトリックス・データ(MD)解析法の使い方←今回
第6章 マトリックス図法の使い方
第7章 系統図法の使い方
第8章 アロー・ダイヤグラム法の使い方
第5章 マトリックス・データ(MD)解析法の使い方
5.3 MD解析法について
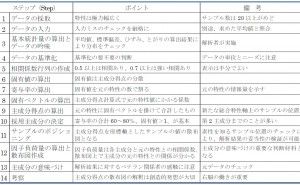
5.3.4 MD解析法のステップの意味と概要
前回のStep 10に続いて解説します。
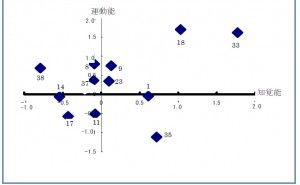
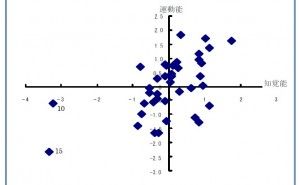
Step 11 : サンプルのポジショニング(主成分得点の散布図作成)
第1主成分と第2主成分を軸とした2次元座標軸上にサンプルの値をプロットすることを“サンプルのポジショニング”と言いますが、アウトプットは主成分得点の散布図の形となります。この散布図におけるサンプルのポジションとサンプルに対して直感的に抱いている印象・評価結果を検討した結果は、Step13で行います。新たな総合的特性である第1主成分と第2主成分の意味づけに大いに参考になるのです。
Step 12 : 因子負荷量の算出と散布図作成
因子負荷量は、各主成分と元の特性との相関係数で、相関行列の形で求められます。この値を、第1主成分と第2主成分を軸とした2次元座標上に散布図を描くことにより、元の特性が両主成分とどう関わっているかが分かります。Step11の散布図と因子負荷量の散布図は、次のステップで行う“主成分の意味づけ”の重要な判断資料です。
Step 13 : 主成分の意味づけ
Step11 の主成分得点の散布図にプロットされたサンプルの位置関係と、日ごろサンプルに対して抱いている印象や評価とを比較検討することにより、第1、第2、両主成分の意味づけを行い、Step12の因子負荷量の散布図を参考に最終決定を下すのが普通のやり方です。ただ、ここで気をつけなければいけないのは、これら解析結果に、関係するベテランなどが、直感的に違和感を持ったときです。
彼らは、往々にして論理的な説明ができない場合が多いので、数理で押し通してしまいがちですが、決定的な間違いを犯す危険性があるので慎重な対応が必要です。確かに、MD解析法の意外な解析結果が、示唆に富む画期的な結論を導くケースもありますが、特性の選定、入力を含むデータの信頼性などが原因のこともあるので、そういった点をチェック確認する柔軟な姿勢が必要です。
Step 14 : 考察
“混沌C”の解明のために取り組んだ場合は、Step11で作成した散布図上に、望ましいサンプル(ベンチマーク)が、解析者が関係するサンプルとかけ離れた位置にプロットされているようなケースが多いのです。
そのギャップの意味と望ましい姿へのアプローチ策の模索を支えるのが、Step11、12で作成した散布図と、両サンプルの元の特性値ですが、数理にこだわり過ぎない柔軟な発想での取り組みが必要す。
MD解析法は、数値解析が主体なので大脳の左半球の働きに依存する手法とされています(「新QC七つ道具」日科技連出版、P.93)が、このステップでは、総合的な、暗黙知に関わる創造的発想が必要で、右半球の働きが重要です。
...