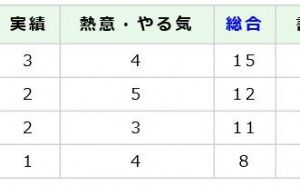
1.判別分析 どこを見れば違いが分かるか?
多変量解析のなかに判別分析というものがあります。重回帰分析や主成分分析ほど有名でないかもしれませんが、非常に便利で大切な分析ツールです。また多変量解析の手法の中では、名が体を表しているともいえます。要は「判別をどうするか? 何をどういう基準で判別するか?」ということになります。我々の身の回りにも結構、それが大事とされる局面があります。直近では4月7日、日本でも新型コロナウイルス世界的流行の影響を受け、7都府県に緊急事態宣言が出されました。
最も厄介なのはこのウイルスの症状です。初期症状ではインフルエンザや風邪、花粉症、通常の疲れなどとあまり変わらないことです。このため、検査結果が出た時点では重症化していたり、他人に移してしまっていたということが多く発生します。残念ながら、この原稿を書いている時でも、いまだに明確な区別方法は見つかっていません。もう少し多くのデータが必要だといえます。
そこまでいかなくても例えば、昔から「アヤメとカキツバタ」や「ヒラメとカレイ」「食用キノコと毒キノコ」など「どこを見れば、違いが分かるのか?」といった判別方法があります。
その違うポイントを知っておけば、判断や予想が楽になります。
その方法につきまして以下に事例を交え解説しましょう。
2.判別対象のデータ例
ここでは、2グループの判別方法に絞ります。就活の時期でもありますが採用にあたって、下記のようなデータが得られたとします。
表1.筆記試験と面接試験の採用合否
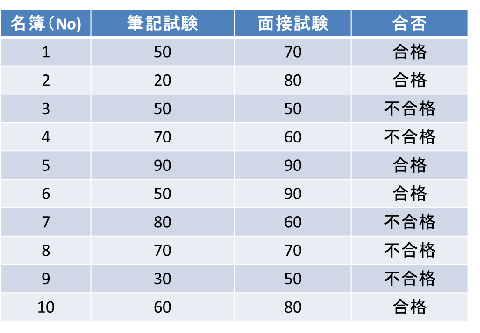
実例数値は「図解でわかる多変量解析」涌井 貞実氏 著(日本実業出版社)から引用
このデータから、筆記と面接の点数が分かれば合否予想が可能になります。
3.判別分析の考え方
多変量解析ではとりあえず、相関を考えることがコツです。そのため、上表をグラフ化します。
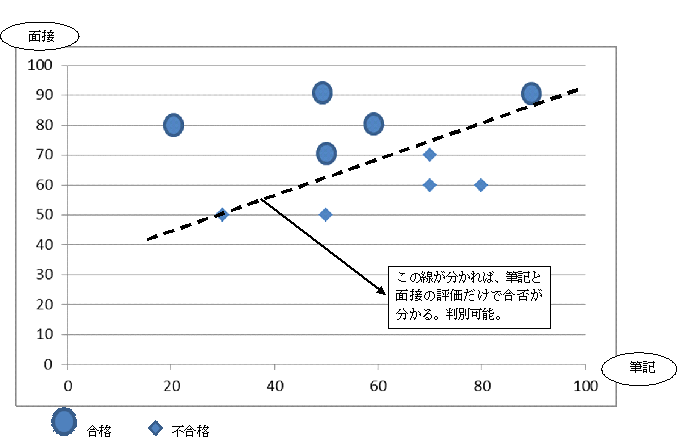
図1.採用判定結果と筆記試験、面接の点数グラフ
上図の点線を数理的に求めることを判別分析といいます。
この方法では境界線を引いているので、線形判別法(線形判別関数法)といわれます。他に、マハラノビス距離を使うものや重回帰分析を利用するもの(実はこれが一番簡単です)がありますが、概念を理解するには線形判別法が理解しやすく、初心者向きです。以下もこの方法について説明します。
4.判別分析の計算方法
差をみるということは結局、差がもっとも出やすい線引きをするということです。差が最も出るということは、二つのグループ(先ほどの例なら、面接の点数と筆記の点数)の差が大きく出るところということです。これを統計用語でいうと、群間ばらつきが最も大きく出るところに線を引け、ということです(群間とは、名前通り、グループ間です。)差をどのように表現するかですが、変動(偏差平方和)を使います。偏差平方和というのも名前通り、偏差=個別データ値―平均値 ですから、この二乗和です。
ただ、ちょっと厄介なのはそれぞれの単純な変動計算をするのではなく、求めたい関数をZとしたとき、Z=a0+a1x1+a2x2として計算します。面接と筆記の得点がa0a1a2関数となって現れます。以下に、計算の流れを示します。
① まず判別したいグループは2つあって、一つは合格グループ:pとします。不合格グループをqとします。
② そのデータは下表のようになります。
表2 合格グループと不合格グループのデータ
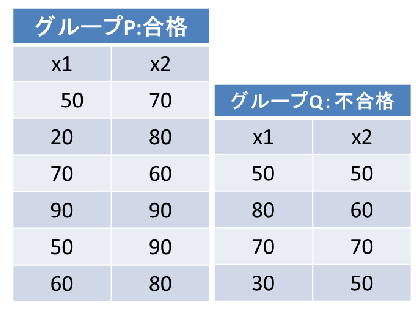
③全変動、群変動を関数表現します。
![]()
ということです。
④

5.判別分析の結果考察
判別関数の係数を見れば、合否に影響が高いものは面接であることが分かります。ただし、これは予想線ですから、実際の合否結果と比べておく必要があります。その...