直交表に関して皆さんからいただいた相談、質問の中からいくつかを公開します。
Q1:直交表で不良率を評価するにはサンプルがたくさん必要ではないでしょうか?
A1:不良対策などで1%以下の不良率を評価しようとすると、直交表の各組合せを数百サンプルずつ作ることになり、現実的ではありません。そこで、以下のいずれかの方法で、少ないサンプル評価を実現して下さい。
方法1:水準を決めるに際して、通常条件より不良が出にくい方向に振ると、全て良品になる可能性が高くなる。まず直交表の多くの要因で結果が悪くなる方向に水準を振り、影響の大きい要因を見極めてから悪くなる水準と反対方向に対策をとり、不良率を評価する。
方法2:例えば直交表L12で評価する時に、不良有無の2段階だと非常に荒い分析になるので、発生した不良をランク別に3~10段階で解析する。
方法3:不良を悪化させる明確な条件がある場合、それを誤差因子として通常条件と悪化条件で2通り直交表実験を行う。つまり「タグチメソッド静特性」実験として実施する。
いずれにしても各実験で不良がゼロだと、得られる知見がない結果になってしまいますので、知恵を絞ってある程度の不良を出すことが肝要です。
また、不良率はいわゆる目的機能で加算性のない特性ですので、本来の技術を開発するには、基本機能を評価するのが早道です。
Q2:直交表で評価する特性が複数ある時はどうしますか?
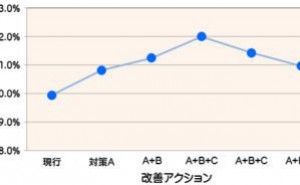
A2:ある特性を改善したい時に別の特性とトレードオフの関係になることがよくあります。理想的には品質工学でいう「基本機能」を見つけ、これひとつで最適解を追求できると良いのですが、慣れるまでは容易でなく、現実的には各サンプルについて、もともと評価しようとした特性だけでなく、影響しそうな他の特性についても測定し、それぞれについて要因効果図を作成してすべての特性を満足する因子水準の組み合わせを検討することになります。
この時実験に組み込んだ因子が少ないと、やはりトレードオフ関係が解消されない危険性が高くなります。複数の評価特性それぞれに効果が期待できる別々の因子を多数同時に評価することで、いずれの特性も満足できる最適解が得られる確率が高まります。
Q3:結果が数値として出てこない直交表実験ではどのように計算しますか?
A3:キズのひどさ、汚れの程度などの官能的特性ですね。例えばキズについては表面粗さ、汚れについては反射率など、計測可能な数値評価による解析を強く推奨しますが、時として感覚による5段階評価点などで解析することもあります。
ただしOK/NGの2段階評価はほとんど機能しません。非常に単純な要因効果図になってしまいます。