1. 高次交互作用とは
高次交互作用の評価を断念することで少ない実験で要因効果を知るためのツールとして直交表があります。工業実験の成果を上げるためにはより多くの因子を扱う事が有効ですが、原理的には掛け算で実験数が増えてしまいますので、すべての結合・組み合わせを評価せず、一部の組み合わせを実験して統計的に要因効果を評価するために直交表が使われます。戦後日本の製造業発展は直交表の効果であると思えるほど効果的な手法で、二水準系、三水準系など多くの種類と使い方があります。
2. 相互作用と交互作用
交互作用の英訳はInteractionで、和訳は、交流や意思の疎通(複数の人の)、相互作用、交互作用、相互影響等とあります。辞典には次のように記載されていました。
例えば添加剤AとBがあり、添加することで製品強度に変化が生じると仮定します。 A、Bそれぞれ単独での効果を[A]と[B]、AとB複合での効果を[AB]と記載すると、相乗、相殺、相加効果としての副作用は次の様になります。
3. 交互作用は難物
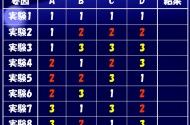
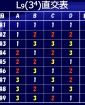
品質工学で主に使用している混合型直交表のL18に「交互作用」が基本的に割り付けることができません。この直交表だけ説明するなら、交互作用のことは説明不要ですが、基本的な部分で動特性のSN比を計算する際には、交互作用が関係します。
つまり、入出力の関係が、誤差因子と交互作用を持っていて、SN比最大化は交互作用の利用ということになります。しかし、内側直交表で制御因子間の交互作用は考えない、というのはどうも直感的に解釈できません。そもそも、要因配置実験では交互作用が重要な解析対象でした。フィッシャーの実験計画法でも、交互作用があるから配置の検討が必要だという解釈でした。
実際に実験してみると、いたるところに交互作用が出てきます。そのことが再現性を悪化させ、実験自体が役に立たないものになってしまうのです。特に制御因子にエネルギー的パラメータ(温度とか電力とかなど)を組み込んで実験すると、実験NO.毎に実験の場がエネルギー的等価性を確保できないため、交互作用の塊になります。それを回避すべく「水準ずらし」により、エネルギー等価性を確保してきました。田口先生の「タイルの実験」などは交互作用問題といっても良いでしょう。
交互作用がないのではなく、交互作用があるから、交互作用効果が出ないように実験を配置することが重要です。しかし、パラメータが離散型(分類データの場合)には積極的に交互作用を利用することになります。
また、A×Bの交互作用効果を計算するとき、ABの変動からAの変動とBの変動を差し引いて、交互作用変動を求めます。つまり、交互作用変動は「残渣変動」といえるのです。要因効果は主効果の組み合わせで表現する方が、妥当性が高いでしょう。結果の解釈を分かりやすくすることが「汎用性」があるともいえます。
交互作用が出ないように実験を配置することができれば、結果の頑健性も向上し、結果の汎用性も上がるでしょう。交互作用は難物です。この交互作用に果敢に取り組むことで、より高いレベルの解釈が可能になります。