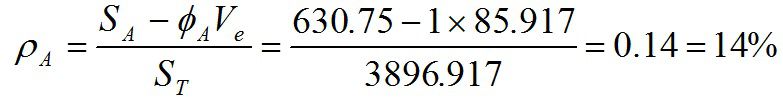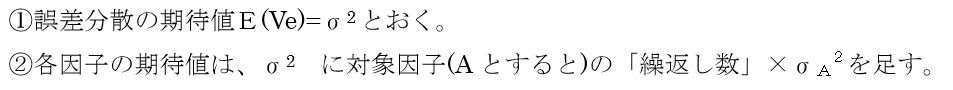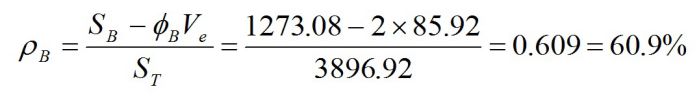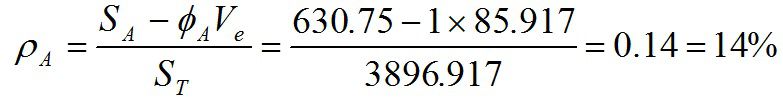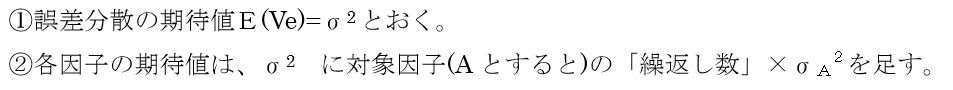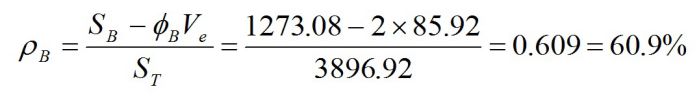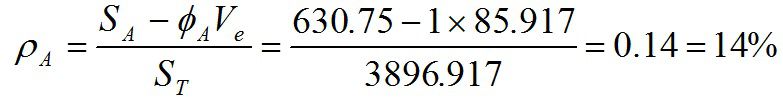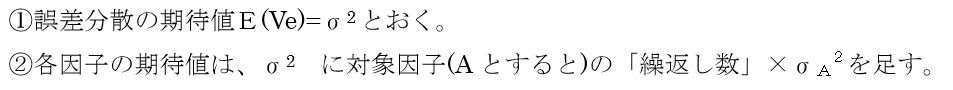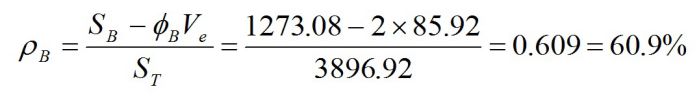二元配置実験や直交表による実験計画法では寄与率という言葉がでてきます。又、回帰分析でも事象の説明がその式でどのくらいできているのかという意味で、決定率とか寄与率とかいうことばがでてきます。ここでは、とくに分散分析での事例をもとに、寄与率の算出根拠を解説します。大抵のテキストは、表1のような寄与率の書き方で表現されています。(二元配置実験)
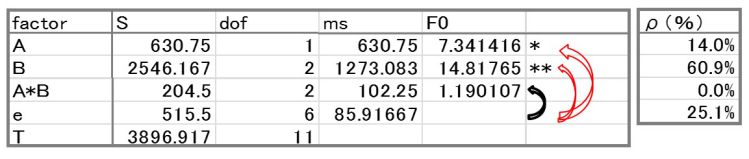
表1 分散分析表と寄与率(ρ)(dofは自由度のことで、以下φやfとも書きます)
このρ(寄与率のこと)は、普通以下の(式1)のように計算されます。
解析に慣れた人なら不思議ではないこの式ですが、「ちょいと見」では、変な式です。純変動の比率であるという説明で済ます場合が多いのです。変動が全データの大きさの程度を表しているので、要因の寄与率というのが変動の比率であるというのは理解できると思います。ただ、純変動の比率であるということです。これもことばのイメージからするとなんとなくわかった気になれます。よくわからないのは、純変動は変動から自由度に比例した分の誤差分散を引いたものだということです。それだけでもよくわからないのに、分母をみると、純(ジュン)変動ではなく、総(ソウ)変動STなので統一感に欠けます。寄与率の計算根拠がわからないという話をきくことがありますが、その理由の大半はこれらのことに関係していると思われます。純変動の比率なので、まず純変動から考えることにしましょう。
その前に、分散分析での分散の期待値について、復習しましょう。これがわからない人は実験計画法のテキストを見てください。難しいことはありません。面倒くさいだけで、定義式から地道に計算していけば導けます。いちいち、こういうテキストのような面倒な計算をしているわけにはいかないので、簡単な書き下ろし方法というものが考案されていて、以下のような方法が昔から使われています。出来上がりの分散分析表(表1)をイメージして下さい。
繰返し数は、全データ数を水準数で割ったものになります。これが、分散の期待値になりますが、ご存知の通り、分散に自由度を掛ければ変動になりますから、変動の期待値も簡単に書き下ろすことができます。これをE(S)と表します。純変動というのは、このE(S)のなかの因子分のみをさします。表1の因子Aについていえば、(自由度が1のため、変動の期待値と分散の期待値は一致しますが、)6σA² が純変動です。Bについていえば、8σB² になります。A×Bも同様です。この部分が、全体の変動に占める比率が寄与率ということになります。ところが、総変動期待値は、純変動の総和に誤差変動分全ての期待値(要は、もとの誤差変動のみでなく、因子のところにくっついていた誤差変動期待値分)を足し合わせるので、総変動と純変動の総和は等しくなります。このため、寄与率計算の時には、分子は純変動ですが、分母は総変動のままでいいことになるわけです。これが、純変動比率なのに、総変動で割る理由です。
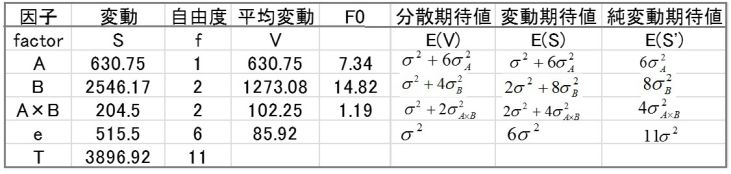
以上を、表にしたものを表2に示します。この表をご覧になりながら、もう一度、本文を読んでいただいた方がわかりやすいと思います。
表2 分散分析における各種期待値への分解
表2からあきらかなように、変動の期待値合計と純変動期待値の合計は一致します。このため、わざわざ純変動の総計をださなくても変動の総計でわれば全体でわったことになります。又、純変動の期待値ですが、因子Bについて説明します。
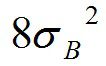
ですが、これは具体的には、表左となりの
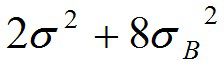
から2σ² を引いたもの計算できます。σ² は誤差分散の85.92です。2は因子Bの自由度でした。
これが、純変動=変動-因子自由度×誤差分散の意味です。AやA×Bについても同様です。
この計算方法により、式1が成り立っています。なお、余談ですが、最近はVでなく平均変動の意味でm.s.が使われます。式1は因子Aの例のため、自由度1です。次の式2に因子Bの例を書きます。
分散の期待値書き下ろしは、以上のように寄与率の算出にも用いられますが、繰り返し実験、分割法、枝わかれ法などの場合の検定手順にも重要なテクニックとなります。