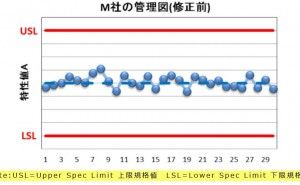
管理図といえば、 通常はシュハートの3シグマ法 (シグマはここでは標準偏差の意味) をさしますが、そのことを知っている人から、逆に質問されたりすることがあります。
例えば
-R管理図の管理限界に関して、単純に3シグマを計算した値とテキストの方法とでは一致しないというものです。
管理図の数理は、素直に標準的なテキストに従えば、難しくなく、むしろ、その見方 (運営) のほうが重要、かつ難しいと思われます。
ただ、基本的な数理の疑問があると、のどに刺さった骨のようで気持ちが悪いというひとのために、わかる範囲で説明します。特にここでは、 前述の-R管理図の管理限界(非常に多い誤解)について説明します。 なお、標準偏差シグマや3シグマの基礎はわかってらっしゃるものとして進めます。 わかってらっしゃらない人は、素直に市販のテキストに従うので、 大きな疑問も誤解も生じないものと思われます。
1. 単純な3シグマ計算と管理図数値表による係数からの管理限界の違いについての確認
例として、群の大きさ n=4 (同一ロットあるいは製造日等)、群の数k=25、よって全データ数Nが100 のとき、平均値が 78 で標準偏差が 0.13 となった場合を想定します。
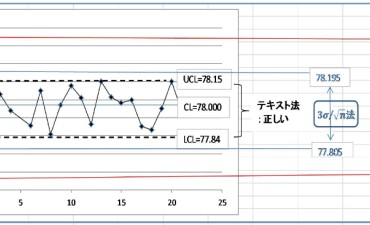
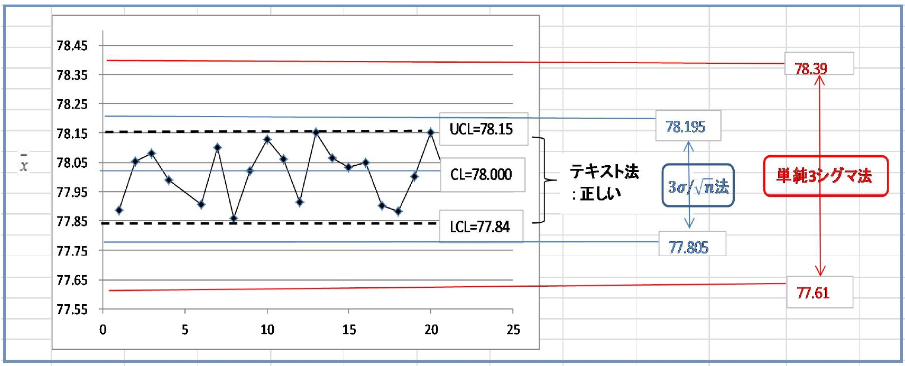
平均値±3シグマで、の管理限界を計算したとすると、78-3×0.13=77.61 から 78+3×0.13=78.39 までとなります。(ここで、この計算を単純3シグマ法と呼ぶことにします)
一方、管理図テキストの係数表、いわゆるA2をみると、A2=0.729。
=0.21 となったとして、 78-0.729×0.21=77.84 が下限で 78+0.729×0.21=78.15 が上限となります。 (ここではこの方法をテキスト法と呼びます) 単純に3シグマから計算した場合は、平均からの片幅が3×0.13=0.39 もあるのに、テキストに従うと 0.729 × 0.21=0.15 となります。 一致すべきなのに、倍半分も違うということがわかります。気がついて質問される方はいいですが、 単純3シグマ法を信じている方は、非常に広範囲での管理限界範囲に守られて、異常に気が付きにくいということになります。
2. なぜそういうことが起こるのでしょうか?
「単純3 シグマ法で標準偏差を算出するときに、分散を全データ数Nで割るとか、全データ数 N−1で割るとかの違いでしょうか?」ということをいわれる方もいますが、データ数が全部で100個もあれば、どうでもいい問題です。 倍半分もの差異は説明できません。そうではなくて、シグマの計算でも、「全データのシグマ」と「群の平均のシグマ」は違うことに大きな原因 (理由) があります。
3. 平均の平均は平均になっても、 平均の標準偏差は全体の標準偏差にはならない
基本的なことの復習ですが、全データの標準偏差をσとすると、群の大きさnとして、群の平均の標準偏差 の関係は以下のようになります。
データの平均()とその標準偏差( 
の標準偏差) との関係は、全データの標準偏差をσとすれば、 
です。基本中の基本です。ということは、-R管理図の管理限界の標準偏差はσでなく、
にしないといけないということになります。ここに、単純3シグマ法とテキスト法の大きな違いの一つがあります。
この場合、σは 0.13でしたから、
=0.13/√4=0.065 この3倍は 0.195 となり、テキスト法の 0.15 に近く なります。(3σ/√n法) (単純3シグマ法では、0.39 でした)
これで、倍半分からは、ずいぶんとリーズナブルな値になりました。しかし、まだ 25%ほど違いがあります。これはなぜでしょうか?
4.R(レンジ: 範囲)からの推定を根拠にしたシグマの計算である
問題にしている管理図は、単独ではなくて-R管理図だということを再認識しましょう。Rをばらつきの基準にしたわけですから、R を基準にした標準偏差を計算しなくてはいけません。 又、現存するデータ100\個 (4個の群が25組) から群平均の標準偏差を計算したとしても、所...
