【目次】
第4章 親和図法の使い方 ←今回
第5章 マトリックス・データ(MD)解析法の使い方
第6章 マトリックス図法の使い方
第7章 系統図法の使い方
第8章 アロー・ダイヤグラム法の使い方
第9章 PDPC法の使い方
第10章 PDCA-TC法の使い方
新QC七つ道具:第4章 親和図法の使い方
4.3 事例に見る親和図法による混沌解明のノウハウ
4.3.3 活用事例の詳細説明
Step 8:表札作り
この“表札作り”について川喜田氏は、「KJ法1ラウンドの諸作業中、最も難しい作業である。そしてこの作業が的確であるか否かで、1ラウンドのまとめの成否が最も決定的に左右される」として最重要視していますが、“KJ法1ラウンド”を“親和図法”と置き換えて、肝に銘じるべきでしょう。
そこで、そういった観点から事例Aの表札をよく観察してみると、1次と2次以降では、表現や内容がずいぶん違っていることに気づくのです。
実は、1次のほとんどは、1N7研で講師のご指導を受けながらのものであり、2次以降は、この結論を実務に活用するため、研修が終わってから、自宅で独自にやりなおした、筆者独自のものなのです。すなわち、2次以降は、1N7研において、グループでのA型図解完成の過程を通じて筆者の脳裏に独自にまとりかけた結論を、表札作りの手順より優先したきらいがあり、その典型がキーワードそのものに近い最終グループの4つの表札に表われています。
ただ、これらは表札として失格には違いないのですが、一方で、このような大胆にして簡潔な本質把握は、B型文章化には必須であるというのが筆者の実感です。すなわち、事例Aの2次以降の表札は、B型文章化には役立ったかもしれないが、A型図解の表札としては、「“表札”と“B型文章化のためのまとめ”を混同した“失敗事例”」といえ、反面教師として参考にしていただきたいのです。
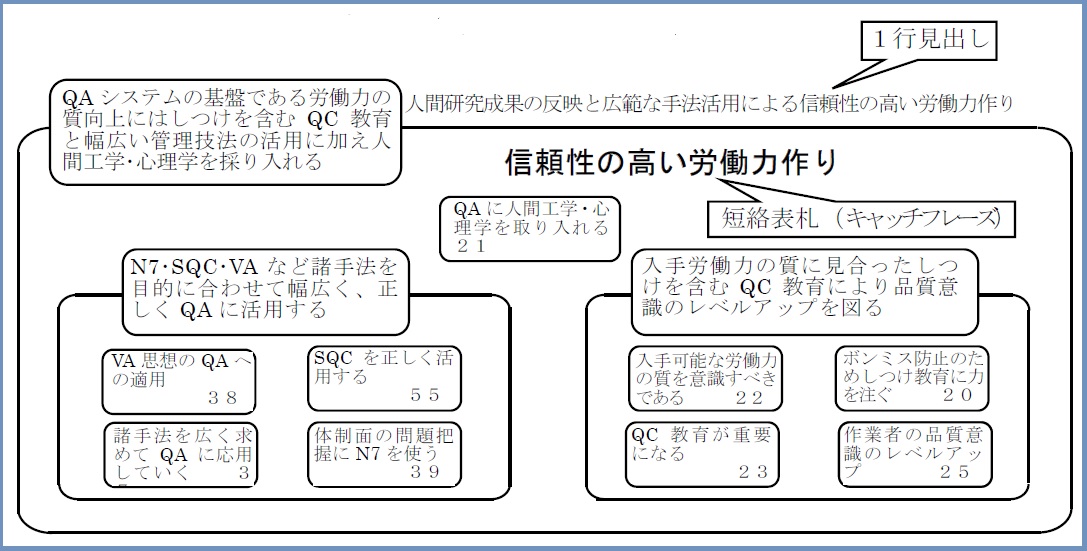
そこで、改めてKJ法の文献にある諸事例をみてみると、そのようなまとめはグループを形成するカードを囲む島どり線上に“1行見出し”という形で書かれており、なかには、島どり線の中に短縮表札ともいえるキャッチフレーズ的な“一言”が大書されているものもあります。
図4-6のA型図解は、B型文章化との関係を見やすくするため、最終グループの“1行見出し”と“短縮表札(キャッチフレーズ)”をA型図解のまとめとして、中央に一覧表の形で表示しましたが、通常は下図(図4-7)のようにグループごとに記入します。ちなみに下図は、最終グループ単位のカード解束事例でもあります。
図4-7.最終グループの個別のカード解束事例
Step 9:グループ編成
事例Aでは、最終的に「高効率QAポリシー」「ファーストルックデザイン」「的確なフォローアップ」「的確な要求品質の把握」といったキーワードで代表される4つのグループにまとまっており、新しいQA体系設計に大いに貢献しました。
しかし、よく見ると、最終のグルーピングには随所に無理が感じられ、結果として、グループ内のデータが十分反映されていないきらいがあるのです。これは、おそらく、グループ数が12になった時点(最終グルーピングの前段階)で、B型文章化の骨格として上記キーワードが頭の中に浮かび、それらをベースに“まとめる形”となったものと思われます。
その結果として、B型文章化はスムーズになされたが、データの語るところが十分反映されきっておらず、A型図解のグルーピングとしては、失敗事例といえるでしょう。
一方、事例Bは、KJ法を勉強しなおしたこともあり、最後まで“データの語るところに忠実に、情念をもって(まとめるという姿勢を排し)データの統合を図った”結果、最終のグループ数は9つと数は多くなりましたが、そのそれぞれが、発想を含んだ具体的な方針を明示しており、親和図法活用の効果がより強く認められます。
A、B両事例からいえることは、“A型図解”は、各データの志をあまねく反映、統合することにより、一見バラバラのデータを、次元の高い“発想”に結びづけようとするものであり、具体的な固有の問題解決を中心とした“B型文章化”とは厳然と区別して取り組むべきであるということです。
Step10:空間配置 Step11:カードの解束 Step12:A型図解
当初、空間配置で苦労したのは、最終グループの相互関連追求を、A型図解の最終レイアウトを念頭に行うためです。この苦労を解消するために工夫したのが、“最終グループごとの独立した紙へのカード解束”であり、これにより、その後の空間配置の変更などが自由自在となり、上記3つのステップをうまくかみ合わせることができるようになりました(図4-7 参照)。
Step13:B型図解
このB型図解は、前節で説明した通り、あくまで、A型図解からB型文章化への移行をスムーズに行うための「補助手段」です。したがって、その形式は、特に定まったものはなく、目的に合ったものを、テーマに従って自由に作ればよいのです。この事例は、テーマのスケールが大きいので、かなり複雑ですが、一般的なスタッフの守備範囲のスケールの場合だと、もっと分かりやすい“連関図”になるのが常でしょう。
そして、この種の連関図には、ループが存在することが多いのです。これは、一般的な“混沌”の原因は、現状ベ...