【目次】
第5章 マトリックス・データ(MD)解析法の使い方←今回
第6章 マトリックス図法の使い方
第7章 系統図法の使い方
第8章 アロー・ダイヤグラム法の使い方
第5章 マトリックス・データ(MD)解析法の使い方
5.2.2 事例テーマ「組立係への新入社員配属基準の策定」
前回に続いて解説します。
(6) 新基準の検証
10項目の評価点を“知覚能”と“運動能”に分けて各人に対する評価を2次元に展開したことにより、組立係への配属不適格者についてベテラン係長と一致した基準を手に入れることができたわけで、この時点では得意満面でした。ところが、この新基準の信頼性をチェックする意味で、座標軸上で最も望ましい位置にあるNo.33について、「No.33は、知覚能、運動能双方に優れダントツだろう?」と組立係長に質問したところ、念のために追加確認したNo.18とともに、「頭は悪くなさそうだが仕事は大したことはなく、中の中もしくは下」との意外な返事が返ってきました。
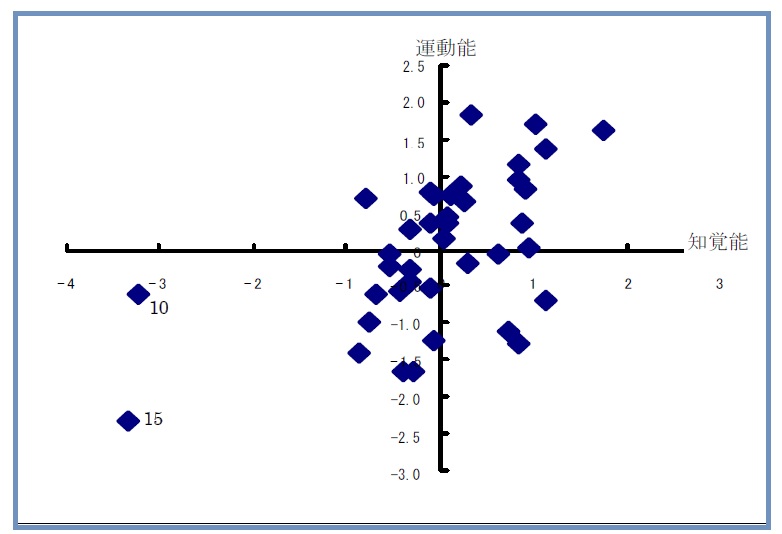
ここにきて、新基準の信頼性に疑問が生じてきたので、さらなる確認のため、39人全員の散布図(図5-2)を作成し、極端な位置を占めたNo.15について配属先の係長に状況を確認したところ、予期に反し、「頭は良くなさそうだがなかなか器用で重宝である」という、これまた意外な返事でした。この結果、この評価基準は、知覚能軸はある程度信頼できますが、運動能軸に対する信頼性が低いといえ、ライン作業者にとり重要な“運動能”に対する信頼性が低いようでは、新基準の採用は無理ということが分かりました。
図5-2 39人全員の2次元評価図
(7) “新評価基準”の模索
まず、2次元評価における“運動能”に対する信頼性が低い理由を考えてみました。試験項目の主目的から3項目の合計を運動能としましたが、経験的に運動能と結構関連する知覚能要因を無視してしまっているからではないかというのが最初に浮かんだ懸念点でした。
この懸念は、一応信頼できるとした知覚能についても、程度の差はあっても、払拭できるものではなかったのです。一方、2次元評価の座標軸を、“知覚能”と“運動能”とする点については経験的に妥当との認識は変わらなかったのです。
とするならば、この評価基準の信頼性を上げるには、各項目ごとに、知覚能、運動能との関わり具合をウエートづけした上で、知覚能、運動能とも10項目全部と関わる数値にする必要があるのではないか、というのが最終的な結論でした。
すなわち、知能という項目についていえば、知覚能に対する評価能力は90%で、運動能に対しては10%、といった具合で、これを10項目について出しておき、各人の各項目の持ち点をこの比率で知覚能と運動能に割り振って知覚能、運動能の合計点を出すのです。
これならいけそうと思いましたが、次の2点に思いあぐねてしまったのです。
- 感覚的に決めたウエートづけで計算し、結果を見てやりなおすのでは非効率です。
- ここまでやるなら、適正検査結果が包含している、注意力や器用さ、正確さといったものも反映したいがどうすればよいか不明です。
まったく世話の焼ける話ですが、事ここに至ってはじめて「いま自分がやりたくてできないことを、数学的にきちんと解き明かす手法こそが“MD解析法”である」と気づき、さっそく取り組むことにしたのです。
5.2.3 MD解析法の本質
今から思えば、この事例は“これぞMD解析法の典型的な活用対象そのもの”なのに大変な回り道をしたのは、当時は、馴染みの薄い数理・数式に惑わされ、MD解析法の本質を把握しきれていなかったからです。すなわち、筆者の前に立ちふさがっていた数理・数式は、単なる手段に過ぎず、「MD解析法の本質は、我々がマトリックス・データに真剣に取り組んだとき必然的に行き着く手立てである」ということに気づいたのです。
読者の中には失笑を買われた方もおありかと思いますが、“筆...