前回の【快年童子の豆鉄砲】(その96)MD解析法による適材適所配属(4)に続けて解説します。
2.事例1にみる「適材適所配属」のためのMD解析法の使い方(続き)
4)事例1解決のためのMD解析法のステップ展開(続き)
Step 11 : 採用主成分の決定
主成分は、計算上元の特性の数だけ求まるのですが、元の特性が持つ情報の大部分をカバーする少数の主成分を採用して解析するのが普通で、採用する主成分の選定基準は、次の2つが一般的です。
- Step8で求めた寄与率の累計が60~80%であること
- 対応する固有値が、固有値の平均値である1より大きいこと
この事例の場合、a.の累積寄与率については、前弾の表78-2で分かる通り、第2主成分まででほぼ7割(68%)をカバーしていますので、第2主成分までを採用することにして解析すれば良いことになります。
b.の固有値の面から見ても、前弾の表78-1で分かる通り、第1主成分の固有値5.10、第2主成分は1.71と1より十分大きいので、上記の選択は妥当と言えます。あと、第3主成分の固有値も1.03と1を超えているのですが、殆ど1と変わりませんので、無理に第3主成分まで採用して、解析を複雑にする必要はないと言えます。
【ポイント】累積寄与率にこだわり過ぎないこと
累積寄与率は、主成分採用判断の重要な要素で高い方が望ましく、80%以上を採用基準とする主張もあります。しかし、それにこだわって採用主成分を3つ以上にすると、サンプルのポジショニングが多次元になり、サンプルのポジションの感覚的な把握が難しく、手法の狙いである“複雑な事象のおおよその見通しと姿の把握を容易にする手法”という趣旨に沿わなくなってきます。したがって、60%を超えておれば、まず第2主成分までの解析を行い、納得のいかない点に的を絞って、第3主成分以降を含めて解析するのが効率的です。
Step 12 : サンプルのポジショニング(主成分得点の散布図作成)
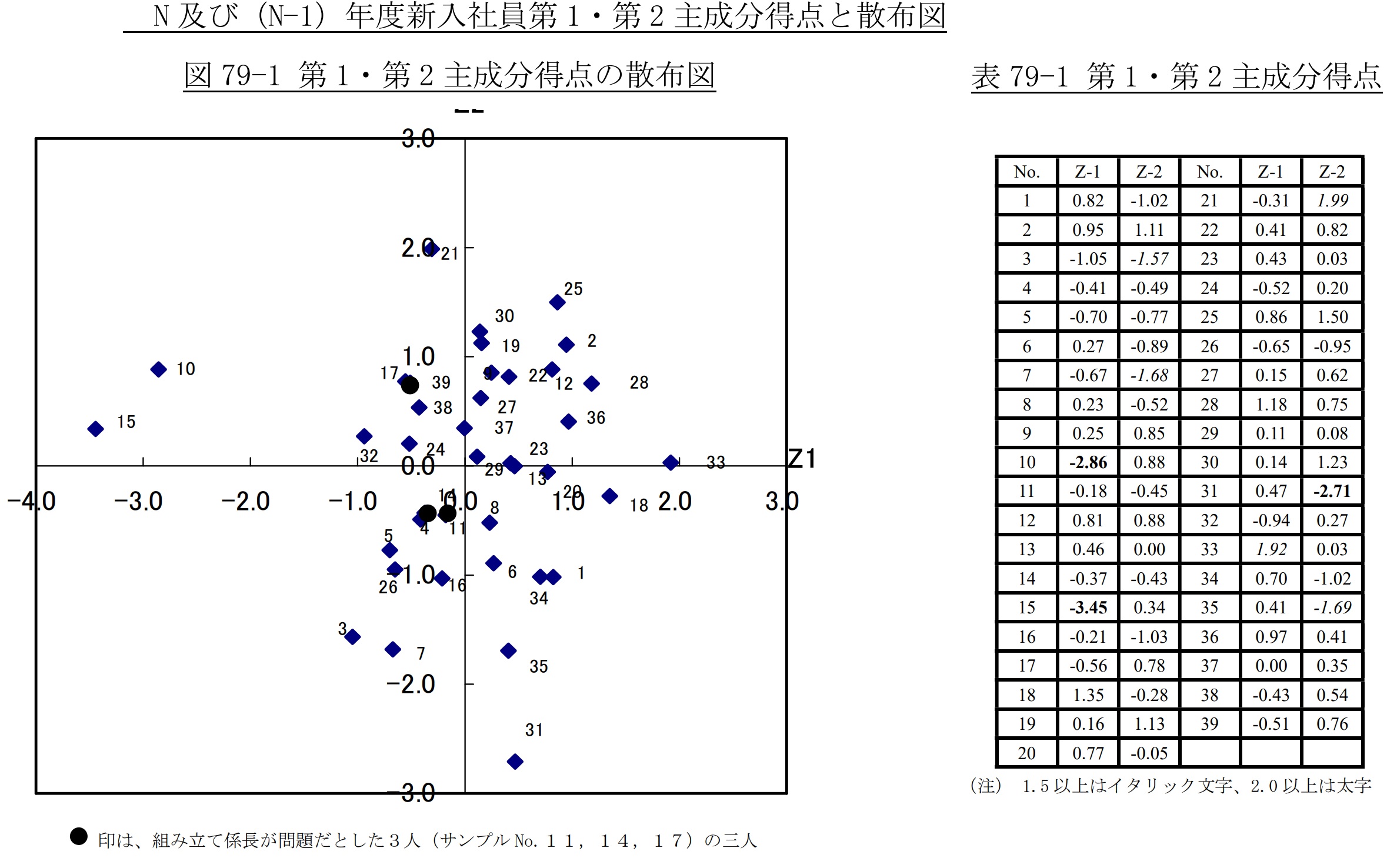
第1、第2主成分を軸とした2次元座標軸上にサンプルの位置をプロットすることを“サンプルのポジショニング”と言い、アウトプットは散布図の形になります。この事例の場合、第一主成分(Z1)を横軸に、第二主成分(Z2)を縦軸に、各サンプルの位置をプロットした散布図を、図79-1に示します。
Step 13 : サンプルのポジショニングから見た主成分の意味付け
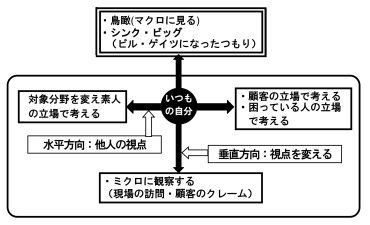
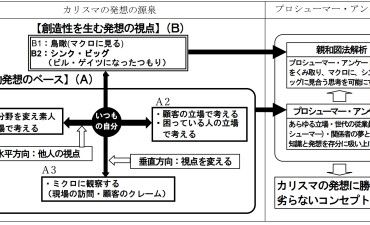
MD解析法は、複雑な対象(この事例では新入社員)を把握するため色々側面からの評価値(この事例では10項目)の相互関連を分析活用し、相互に独立した少数の総合的特性値(主成分)にまとめることによって、複雑な事象のおおよその見通しと姿の把握を容易にする手法なのですが、そのためには採用主成分、この事例では第一主成分(Z1)と第二主成分(Z2)の意味付けをする必要があります。
この事例の場合、(N-1)年度入社者には1年間の観察結果、N年度入社者には、1ヵ月とはいえ新入社員教育で濃密な観察結果があり、漠然とではありますが各サンプルの総合能力をかなり的確に把握できていますので、散布図上のそれぞれのサンプルの位置を検討・吟味することにより、第一主成分が「知覚能」、第二主成分が「運動能」との意味付けが出来ています。
一般的な場合も、各サンプルに対する総合的な把握がかなりのレベルで出来ているのが普通ですので、散布図におけるサンプルの位置をつぶさに検討することにより、かなりの精度で主成分の意味付けができるものです。
要するに、MD解析法に頼るテーマの場合、複雑な解析対象を理解しようと、多くの側面から調査検討して手に入れたマトリックスデータから把握できる内容が、あまりにも漠然としすぎてテーマ解決につながらないものの、各サンプルに対する理解はかなり明確に把握できていますので、第一主成分、第二主成分を軸とした散布図上のサンプルの位置をつぶさに検討することにより、両主成分の意味付けが可能ということです。
Step 14 : 因子負荷量の算出と散布図作成
因子負荷量の“算出”としましたが、これまでと同様、算出にかかわる数学的な面はソフトに任せ、ソフトが算出した因子負荷量の意味や使い方の説明をします。因子負荷量は、各主成分と元の特性との相関係数で、相関行列の形で求められます。
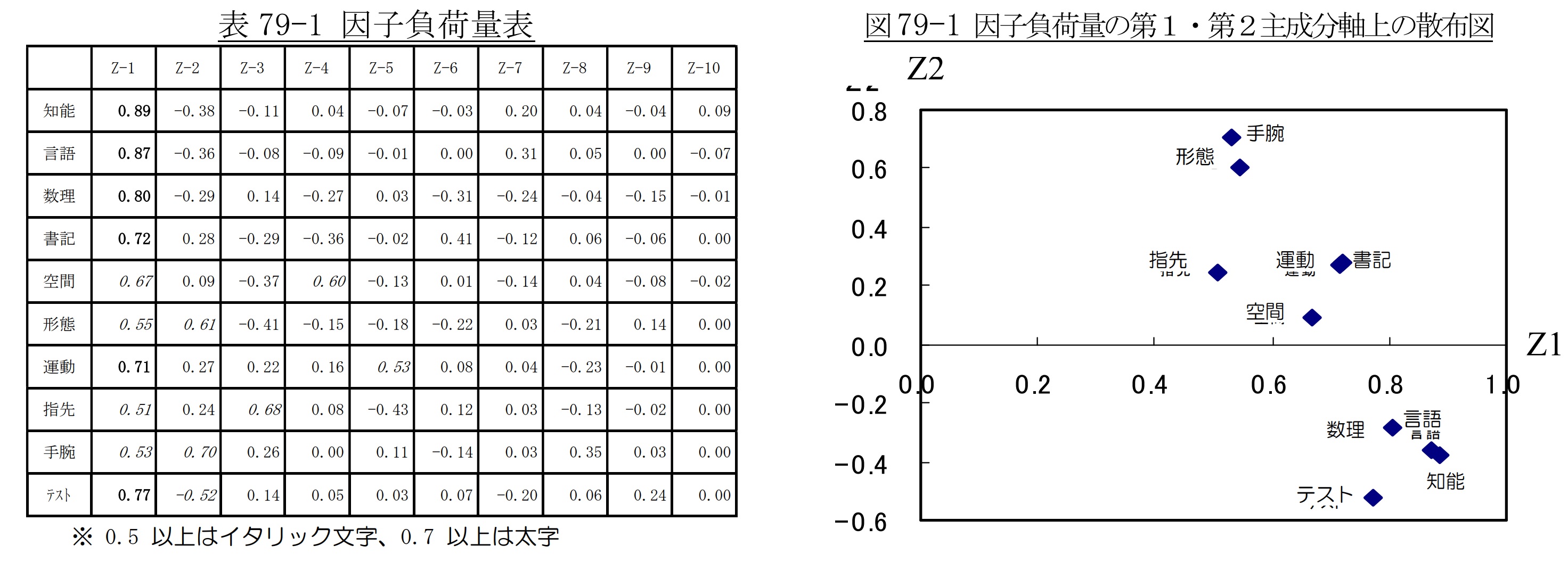
従って、採用主成分である、第1主成分と第2主成分を軸とした2次元座標上に因子負荷量の散布図を描くことにより、元の特性が両主成分とどう関わっているかが可視化されて分かり易くなりますので、Step15でご説明しますが、主成分得点の散布図から読み取った主成分の意味付けの検証に使うことが出来ます。
この事例について、因子負荷量の算出結果を表79-1に、その散布図を図79-1に示します。
次回に続きます。
M
...