1. 数理統計手法の活用能力
今回は「企業が社員に求める能力10項目」(表84-1)にもあり、現在の仕事を向上させるための3つの“能力”の内3番目「数理統計能力(I)」の説明です。この項目の場合の能力は、数理統計手法の活用能力のことで、本人の理解能力による限界はありますが、基本的には100%育成可能ですので、必要に応じて本人の理解状況を見ながら、成果と結び付けた育成により、本人のやる気につなげるのがポイントになります。
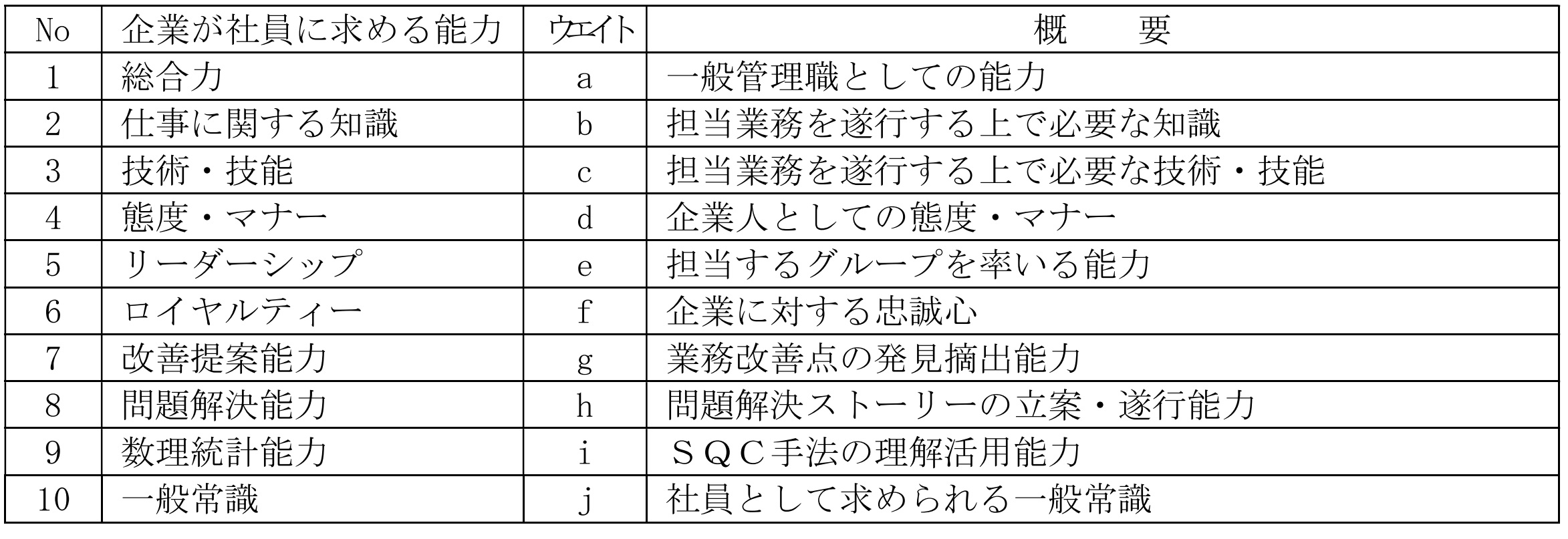
表84-1 企業が社員に求める能力10項目
2.「数理統計能力(I)」の育成ステップ
この数理統計能力の基本となるのが「数理統計手法の活用能力」で、企業における改善活動レベルを決定付けると言っても過言ではありませんので、各企業が力を入れているのですが、基本的に集合教育です。この集合教育の場合、知識は身についても実務への活用につながらず、掛ける努力に対して効果が今一つと言うのが一般的です。
その点、OJCCは、身近なテーマ解決における必要性を感じている本人のニーズに合わせた活用の中での育成ですので、手法活用が身近なものとして完全に身に付いて、次からは自主的活用が可能な育成ですので、下部の「数理統計能力(I)の育成ステップ例」(表93-1)を参考に育成して頂ければと思います。
ただ、ステップをご覧になって、算数レベルのチェックは不要と思われるかもしれませんが、最近はとんでもない算数音痴も居ますので、仕事に支障を来たさぬための確認ステップと言えます。育成ステップの備考欄の詳細は注記に譲るとして、包括的レベルについて下記しますので、ご理解の参考にして頂ければと思います。
1)算数のレベル
いわゆる数の取り扱い四則、加減乗除のことで、出来て当たり前なんですが、万一不得手で間違いがあった場合、数字は仕事で重要な意味を持つ場合が多く、間違うと大きな損失を生みますので、この確認は大切です。特に、文科省の検定に合格した来春(令和4年)の高校の数学Ⅰの教科書に、二桁引き算や九九の説明に30ページも使うご時世であることは念頭に置いておく必要があると思います。
2)代数のレベル
仕事ではよくあることなんですが、複数の要素が対象になる問題解決に取り組む場合、数字の代わりにXやYと言った文字を与えて計算、解析することを言います。上述の「算数レベル」のチェックなしにここに入りますと、もし分からなくても、本人としては今更分からないとは言い難いだけに、育成が思ったように進みませんので、そういった事態を避ける意味でも「算数レベル」のチェックは大切です。
3)SQC(統計的品質管理)手法活用レベル
この項目の主眼はここにあり、典型的な手法をステップ例として挙げていますが、企業によってはこれ以外が必要な場合もありますので、その場合はステップを追加して頂ければと思います。
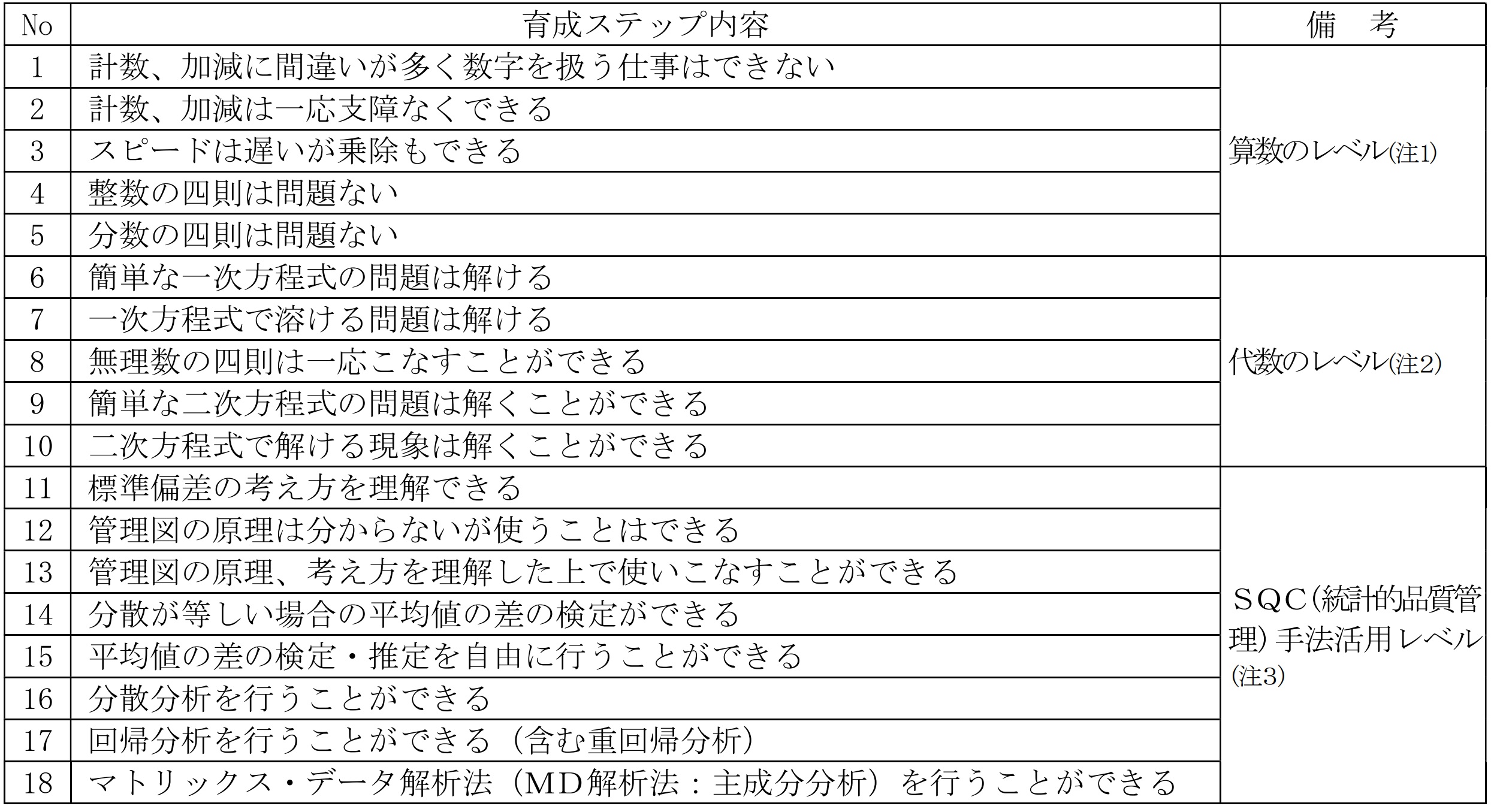
表93-1 「数理統計能力(I)」の育成ステップ例
(注1):計算の四則なんですが、対象が整数の場合と分数の場合があります。整数の場合は、チェックも育成も特に問題ありませんが、分数の場合は、チェックも育成も系統立ててやろうとすると結構面倒ですが、仕事で必要になったところだけを取り上げて、そこのところが使いこなせるようになったところで系統立てた育成に入るのがいいと思います。
(注2):算数レベルの四則は必須ですが、職場の問題解決には、数学的な考え方とそれを具体的な形にして解決に導く手段が必要です。その基本となるのが、無理数の四則と二次方程式に代表される代数です。これはかなりレベルの高い話になりますので、育成対象者は限られますが、職場の問題解決途上で、これ等の活用に強い興味を持たせたうえであれば、日本の高校教育を修了したものであれば、育成が可能のはずですので、こういった人材の育成が、これからの中小企業にとって必須との認識の下頑張って頂ければと思います。
(注3):このSQC手法の活用能力こそがこの項目の真髄で、特に、中小企業の多くを占める製造業に取り非常に重要です。まず、標準偏差の考え方により、製造品質の実情を的確に把握し、それを基準に管理図法で日常の品質を管理し、品質改善を認めたら、改善活動を行い、その効果を、分散分析と平均値の差の検定で把握することになります。今ひとつ製造品質で重要なのは、短期間の上記活動では把握できない長期的観点からの品質の変化の把握で、それを明確に把握できるのが回帰分析です。上述した内容を理解した上で、職場のニーズに合わせて順次取り組み、育成して頂ければと思います。最後にある「MD(マトリックス・データ)解析法」は、仕事上で生じるデータがどんどん複雑になる中、その解析に必須なのが、多変量解析なのですが、その中で最もポピュラーで、活用効果が期待できるのがこの「MD解析法」です。かなりハイレベルの話ですが、考え方さえ把握できれば、今まで活用の妨げであった複雑な計算は、最近はパソコン用ソフトで一挙に図の表示迄手に入れることが出来るのがありますので、ぜひ挑戦されればと思います。
3. ふさわしい手法をテーマに即してガイド育成すること
この項目の場合、適切に活用すれば効果的な手法が多く存在しますので、それらを活用できるように育成するのがポイントになりますが、よく実施される集合教育は、労多くして効果が少ないのが常ですので、此処にご紹介するように、手法が効果を発揮する仕事の中で、育成するのが得策です。従って、各ステップのふさわしい手法を、具体的テーマに即してガイド育成するのがポイントになります。
次回に続きます。
...