前回の【快年童子の豆鉄砲】(その95)MD解析法による適材適所配属(3)に続けて解説します。
2.事例1にみる「適材適所配属」のためのMD解析法の使い方(続き)
4)事例1解決のためのMD解析法のステップ展開(続き)
Step 7 : 固有値の算出
固有値の“算出”としましたが、ここでは、算出にかかわる数学的な面はソフトに任せ、ソフトが算出した固有値の意味や使い方の説明をします。
固有値は、“eigen (固有の)-value (値)”の訳で、その意味するところは「事象本来の固有の姿をよく現わす形にする値」で、数学的には「主成分得点の分散」です。何故かと言いますと、“事象本来の固有の姿をよく現わす”ための新しい特性が“主成分”で、よく現わす度合いは、サンプルごとに求めた“主成分得点”のばらつき(分散)の大きい方が有利だからです。
したがって、固有値が最大の主成分が、“事象本来の固有の姿を最もよく現わす新しい特性”ということになり、“第1主成分”と呼ばれ、以降、“第2主成分”、“第3主成分”・・・となります。
固有値は、元の特性の数だけ求められ、その合計も、元の特性の数に等しいので、固有値の平均は1となります。したがって、固有値が1以下ということは、その主成分の持っている情報が元の特性以下ということになりますので、値が1を超える固有値に対応する主成分を採用して解析するのが普通です。
この事例の場合の固有値の算出結果を表78-1に示します。これを見ますと、1を超えるのは第3主成分(Z3)までなのですが、第3主成分はほとんど1に近いので、この事例の場合、固有値の観点からの採用は第1、第2主成分になります。
表78-1 固有値の算出結果

Step 8 : 寄与率の算出
寄与率の“算出”としましたが、Step7と同様、算出にかかわる数学的な面はソフトに任せ、ソフトが算出した寄与率の意味や使い方の説明をします。
寄与率とは、固有値を元の特性の数で割った値で、固有値が対応する主成分が、元の特性のいくつ分の情報を持っているか、即ち、新しい特性である主成分が持つ情報量の大きさを示す値と言えますので、解析に際し、主成分をどこまで採用するかの重要な判断基準になります。
要するに、主成分分析法(MD解析法)は“複雑な事象のおおよその見通しと姿の把握を容易にする手法”で、この“おおよそ”の目途が問題なのですが、寄与率の累積が60~80%となる主成分を採用するのが一般的です。この事例の寄与率算出結果を表78-2に示しますが、この事例の場合は、見ての通り、累積寄与率が68%になる第2主成分(Z-2)までを採用することになります。
表78-2 寄与率算出結果

Step 9 : 固有ベクトルの算出
固有ベクトルの“算出”としましたが、Step7、Step8と同様、算出にかかわる数学的な面はソフトに任せ、ソフトが算出した固有ベクトルの意味や使い方の説明をします。
主成分は、元の特性の特徴を要約した総合的特性値と言えるのですが、具体的には、元の変数それぞれに重みをもった係数を掛けて足したものです。この元の特性の特徴を要約するために掛ける“重みをもった係数”が固有ベクトルなのです。
固有ベクトルはその性質上固有値と同時に算出され、各サンプルの主成分得点算出式で元の特性値に掛ける係数の役割を果たすのですが、その数値自体はここでは使いませんので表示は省略します。
Step 10 : 主成分得点の算出
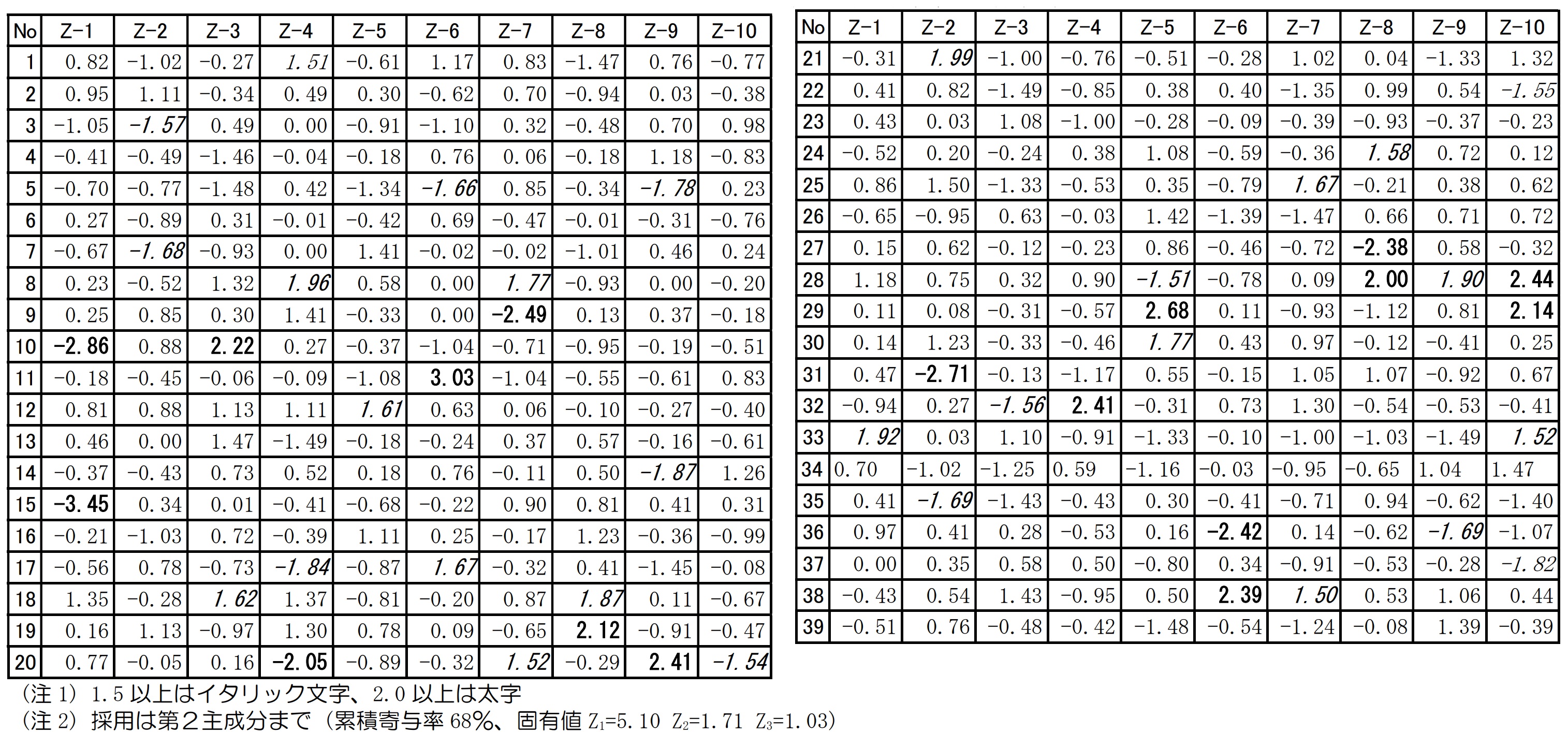
主成分得点もソフトで出てくるのですが、中身は、サンプルの元の特性値にStep 9 で求めた固有ベクトルを係数として掛けたものの合計です。
この値は、新たな総合的特性である主成分軸上に占めるサンプルの位置を示すもので、第1主成分と第2主成分を縦軸と横軸にしたグラフ上に、主成分得点に従って各サンプルの位置をプロットした散布図を観察分析することにより...