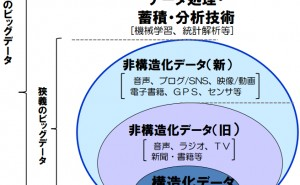
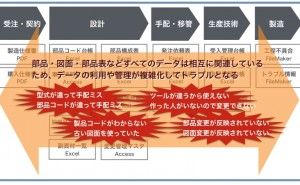
ビッグデータの活用と声高に叫ばれています。無論、自動的にビッグデータが取れれば多いに越したことはありませんが、スモールデータでも十分に検証できます。
私は顧客アンケート調査の設計から実査、分析までを頻繁に行っていますが、今回は最適な回収データ数について解説します。
よく、データを何人取ったら有効でしょうか?と質問を受けます。データはたくさん取った方がいいなど、いろいろな意見が飛び交いますが。データ数50人よりデータ数100人。三桁のデータを扱うことを目標にしましょう。特に根拠はありませんが、調査データが 50人よりは 100人の方がよさそうです。
100人と200人となると、多い方がいいですが、人数が多くなるとそのための工数や費用が掛かります。そこで、統計解析には誤差を推定することが可能です。この考え方から必要なデータ数を考えて見ましょう。
統計学の中に少ないデータで全体を推定することができます。その時の前提としては
- データが少ないと全体の誤差が大きい。
- データが多いと全体の誤差は少ない。
ではどの程度でしょうか。比率の誤差は簡便法で 1/ √nで推定できるのです。
100人の比率の誤差は 最大 10%、400人の比率の誤差は最大 5%、1万人の比率の誤差は最大 1%になります。
例としてアンケート調査等で回答の比率の結果:男性 50%と結果が出ました。
その時、100人の場合は ± 10%、400人の場合は ± 5%、1万人の場合は ± 1%。
100人ですと、± 10%も誤差があるので、問題が出てきます。400人ですと、± 5%の誤差なので、統計でよく使う95%の許容範囲に入ってきます。
また、アンケート調査の段階評価や得点評価において平均値を使うことも多いでしょう。
平均値の誤差は、簡便法で 2/ √nで推定できます。
100人の場合、誤差は ± 0.2点、400人の場合、誤差は ± 0.1点、1万人の場合、誤差は ± 0.02点になります。
400人ですと、平均値 3.5点の結果は全体では 3.4点 ~ 3.6点 にあることが推...