L9直交表と二元配置実験の交互作用関係

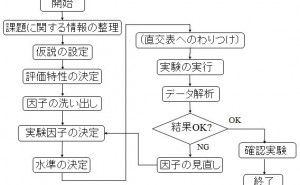
　ここでは、変動の計算方法が理解されていることを前提に説明いたしますので、計算方法をご存知でない方は、そちらを先に学習なさってください。まず、L9直交表の構成ですが、下表のようになっています。

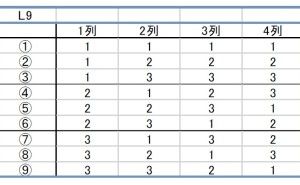
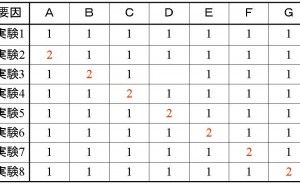
表1　L9直交表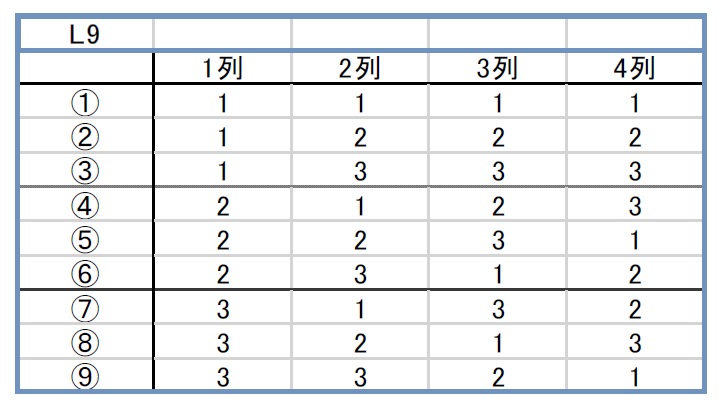

　①から⑨は実験Noといわれるものであり、これが実験回数に相当しています。列番の下の数字は水準記号です。

　このL9直交表は3水準であることと、実験回数が少ないこともあり、比較的多く利用されます。ただし、その使い方はおおむね因子数が３か４です。どうしてそうなるかについては、別の機会に解説致します。

　今回は、このL9直交表に交互作用を割り付けると、工数的に損得があるのかどうかということです。要は2元配置3水準なら、9回でも交互作用は出ません。このことは、よく理解されているようです。なぜかといえば、誤差と交互作用とを分離しなければ交互作用が求められないから（よって実験回数は18回）、というのが市販テキストの基本になっているからだと思われます。ところが市販テキストには、L9直交表の交互作用について、次のような記述が多いのです。

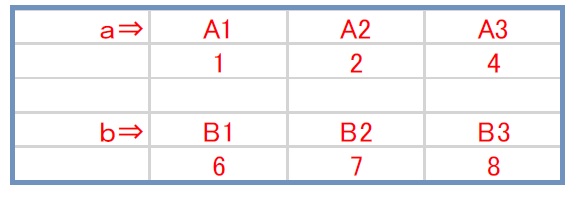
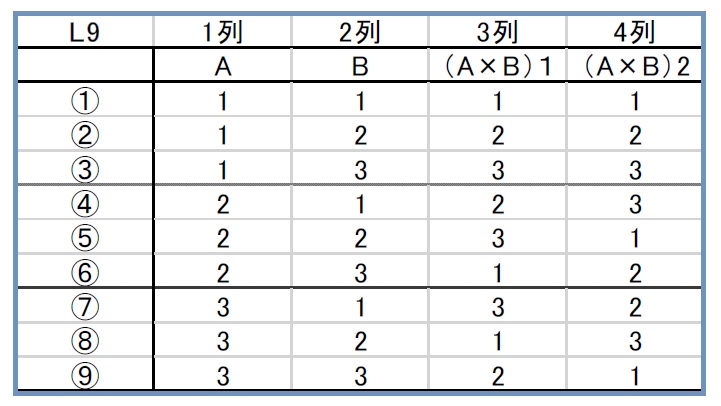
　「L9直交表で2列に因子を割り付けると、その交互作用は残りの2列に現れる。」

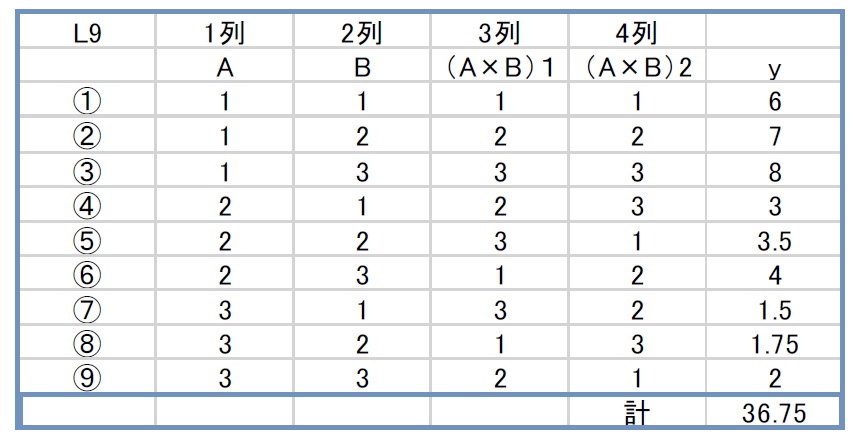
　例えば、1列目に因子A、2列目に因子Bを割り付けると、残りの3列目と4列目に交互作用A×Bが現れるということです。1列目に因子A、3列目に因子Bを割り付けると、交互作用は2列目と4列目に現れます。

　これはこれで正しいのですが、このことと9回の実験だけで、交互作用が解析できると思ったら間違いです。もしそうであれば、3水準二元配置実験の半分の工数で交互作用が分かることになりますがそうはいきません。

　L9直交表での交互作用といっているものは、表現が違うだけで誤差と交互作用が込みで入っています。わざわざそのように断わっていないだけです。しかし、初心者は交互作用が求められるので、3水準二元配置実験よりはL9直交表のほうが、少ない実験回数で交互作用を求められるものだと勘違いするのです。では事例で説明しましょう。

　説明用として特性値が計算で求められるように、ｙ＝b/a とします。（a+b, a+b^2では交互作用は出ません。一方、上式では非線形交互作用が発生します）　bは因子B、aは因子Aの水準値であるとし下表のように仮定します。

　表2　水準表

　L9直交表の第一列に因子Aを第二列に因子Bを割り付けたとします（何列にでも構いません）。下表のようになります。

表3　割り付け例

　この表現の仕方が誤解の元です。計算式に従ってL9直交表の実験番号ごとに数値を入れたのが下表です。

　表4　実験結果（計算結果）

　変動の計算をやってみましょう。この計算方法は省略します。ｍsは平均変動で昔の人は分散といっていました。ｆは自由度です。分散分析表は下表5のようになります。

　表5　L9直交表分散分析　　

　正確にA×Bが出ているではないか、と思われるでしょうが、どこにも誤差がありません。誤差がない限り、何と比較して有意だの、寄与率だのと言えるのでしょう。誤差はこのA×Bに入っています。このままでは抜き取れないのです。抜き取って分離するには、もう一度実験を繰り返して、そこから生じる誤差を計算しないといけません。よって、2回繰り返せば二元配置と同じ18回の実験になります。二元配置の場合も計算しておきましょう。

　表6　二元配置実験結果

　この分散分析は下表7のようになります。

表7　二元配置の分散分析

　表5と表7は一致しています。変動分解の方法は若干違うにせよ、結果は一致しています。表7では、通常、A×Bを誤差にした表現をしています。要はL9直交表の場合は、交互作用という言葉を使い、二次元配置の場合は、誤差という表現をしているだけです。誤差か交互作用かは、繰り返して分離しないといけませんから、L9直交表と二次元配置での実験工数は変わりません。損も得もしません。

　これらは、本当は自由度の計算を考えれば、一目瞭然です。3水準で因子数が2個ですから、L9直交表...