
♦ 階層的構造から代替案を評価
1. 1対比較表を使った行列計算から選定
AHP(Analytical Hierarchy Process・階層分析法)は、主観に基づく意思決定を構造的・数値的に扱うことで、人々の合意形成や意図の伝達に寄与する手法です。1970年代からトーマス・サーティが政策科学の分野で提唱し、その後多くの方面で応用されてきました。
簡単な例を図1.に示します。A社、B社、C社のどの製品を購入するか?という選定問題です。上段に意思決定の総合目的、中段にそのための評価基準、下段に代替案(選択肢)の3階層を設定します。
それぞれの重要度(もしくは優位性)が図1.のように与えられた場合、図2.のように行列計算をして総合重要度を求めます。各社製品の評価基準ごとの重要度(優位性)に、評価基準自体の重要度を掛けて総和をとったものが総合重要度です。この場合、A社製品が最も高得点で購入選定となります。評価基準を変えれば、就職企業の選択などにも使えます。
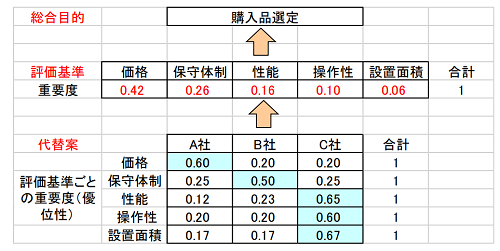
図1.階層構造

図2.総合重要度計算方法
各重要度の算出方法を図3.と図4.に示します。1対比較法を用います。各升目(ますめ)に、行の基準の列の基準に対する重要度(優位性)スコアを、図5.サーティの1対比較表に従って記入し、対角位置にはその逆数を記入します。表にはない中間値(偶数)を用いても構いません。各行の幾何平均(図3.であれば5つのスコアを掛けた5乗根)を算出し、その総和で各行を割って正規化したものが重要度となります。
※計算方法の根拠は紹介記事の範疇(はんちゅう)を超えるので割愛します。計算方法は他にもあります。
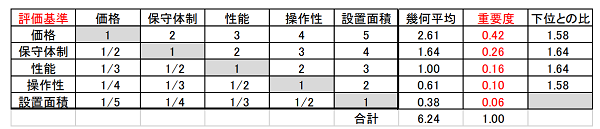
図3.評価基準の重要度算出
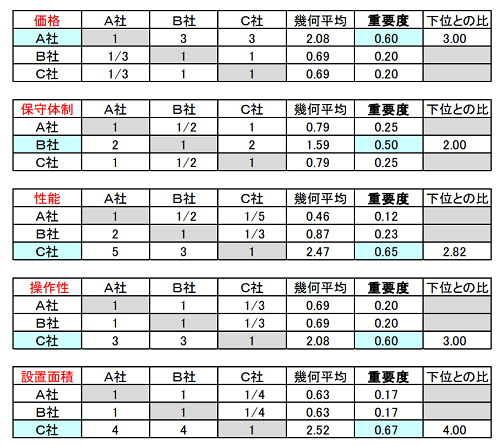
図4.評価基準ごとの重要度(優位性)

図5.サーティの1対比較表㊧と図6.西本の1対比較表
このように、AHP を用いると意思決定の根拠が明確かつ数値化されるので、複数人の1対比較を集計・平均すれば集団の合意形成もスムーズになります。工学分野では QFD(品質機能展開)の最上流である顧客要望の数値化にも使われます。ただ、1対比較する要素が増えると升目が指数関数的に増えるので、要素数は最大9が推奨されています。
2. AHPも完全ではない ~ 注意点と改善策
以上が文献や学会で紹介される AHPのサマリーですが、実務家視点で以下の注意点を挙げておきます。
図5.サーティ表に従って記入すると、少しの差を拡大した重要度となります。図4.を丹念に見ると、“少し重要3”を記入すると重要度は3倍、“ほんの少し重要2”は重要度2倍です。図3.で、隣り合う評価基準の差は“ほんの少し重要2”ですが、重要度の比は概ね1.6倍です。“価格”は“性能”より“少し重要3”ですが重要度は0.42対0.16(2.6 倍)の大差です。その結果、優秀だが価格が“少し劣る”C 社は破れ、価格のみが“少し優位”な A 社が選定されます。レーダーチャートだと、また違った判断になるでしょう。
では、少しの差を拡大する利点はどこに有るのでしょうか?AHP はもともと政策科学の分野で考案されたとされています。公共事業の意思決定で、公園緑地か図書館か体育館か?といった場合、35:33:32で公園に決定というより、数学的検証の結果50:30:20で公園とした方が行政は進めやすいでしょう。1対比較表で、結果をある程度恣意(しい)的に操作できるという事ですが、各種統計処理でも設問やその他操作で同様の事はあると推察します。
しかし、工学分野でサーティ表を妄信するのは問題ありです。図3.は顧客要望の把握でも利用可能ですが、“価格”は“性能”より“少し重要”という顧客の気持は、重要度0.42対0.16(2.6 倍)として開発に伝わります。この差を、QFD(品質表)で下方展開して良いのか?顧客要望に即した製品が開発されるのか?違和感がぬぐえません。このような結果になるのはサーティ表に従うからですが、文献・学会などではサーティ表がバイブルになっているようで、この点についての議論を目にしたことはありませんので、以下に改善策を提示します。
要は、主観とマッチした重要度になるようにすれば良い訳です。対処療法としては、妥当な1対比較表を作る事です。図6.に例を示します。図7.に、図6.西本表を使った場合の例題結果を示します。C 社が選定されました。隣り合う評価基準の差“ほんの少し重要”の重要度比は概ね 1.2 倍となり、常識的なところと思われます(1.2倍に違和感を覚える人は、1対比較表を自由に変えて下さい)。

図7.西本の1対比較表による総合重要度結果
ただ、重要度の結果が1対比較表に影...



















