本記事は「あいまいな主観を数値化して意思決定を行う:AHPとは」(以後、前記事と表記)の続編となりますので、そちらをまずお読みください。
前記事で、AHP(Analytical Hierarchy Process:階層分析法)の問題点として“(主観の)少しの差を拡大した重要度を算出する”事を挙げ、顧客要望の把握などで利用する場合のリスクを指摘しました。そこで、顧客の主観とマッチする重要度を把握するための改善策として、“価格と性能の重要度が6:4と感じるなら、それをそのまま1対比較に使う”アイデアを紹介しました。このアイデアに基づく手法を SPC(Spec Priority Confirmation :スペック優先確認)と呼び、今回はその手順を解説します(参考文献:特開 2012-099074)。
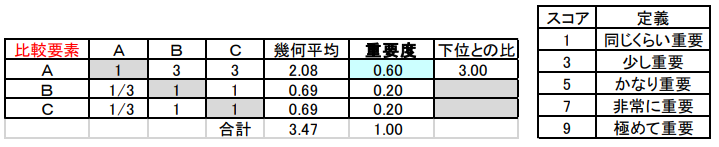
図1に SPCにおける1対比較記入例を示します。AHP のような図6「サーティの1対比較表」は使いません。価格と性能の重要度が6:4と感じるなら、価格行と性能列の交点に6、対角位置の性能行と価格列の交点に4と記入します。10点スコアの按分(あんぶん)を基本とするので、対角線は自分どうしの比較なので5とします。この方法なら、サーティ表の“少し”や“かなり”といった曖昧(あいまい)表現に惑わされる事なく、主観をストレートに記入できます。
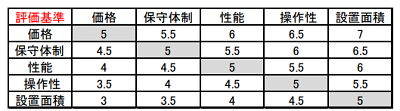
図1.評価基準の1対比較 (按分スコア)
図2に SPC 重要度の算出方法を示します。図1の行の按分スコアを、比較している相手(対角位置)のスコアで割ります。価格行と性能列の交点は 6/4=1.5、性能行と価格列の交点は 4/6=0.67 となります。対角線は自分どうしの割り算で1となります。その後は前記事と同様、各行の幾何平均(5つのスコアを掛けた5乗根)を算出し、その総和で各行を割って正規化したものが重要度となります。
この例では、隣り合う基準の1対比較スコアは全て5.5:4.5(比 1.22)としましたが、算出された隣り合う重要度の比は1.23 となり、SPC重要度は主観のスコア比と大きく乖離(かいり)しない事が分かります。顧客要望をQFD(品質表)に入力する際、顧客の気持ちの少しの差を拡大する AHP重要度(サーティ表)を用いるより、気持ちの差をストレートに反映するSPC重要度を用いたほうが、より要望にマッチした製品が開発されると期待されます(前記事図3のAHP事例と見比べて下さい)。
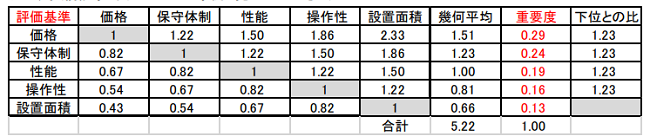
図2.評価基準の SPC 重要度算出 (按分スコア比)
次に、重要度算出のロジックを図3を使って概説します。重要度は総和が1となるように正規化しますので、絶対値ではなく、各重要度の比が分かれば良いのですが、各比較要素 A・・・E の絶対値重要度 a・・・e を仮定します。a・・・e の真値が最初から明確なら1対比較などする必要は有りませんが、値が曖昧(a=真値+誤差)なので、1対比較表から真値に近い値を推定したいわけです。
そのための手順が、前出の“行の按分スコアを、比較している相手(対角位置)のスコアで割る”という操作で、図3では各升目に a/c などの分数(絶対重要度の比)で示されます。次に、誤差を平準化して真値に近い値を推定するために“各行の幾何平均を算出”すると、便利なことに分母がすべて同じ5乗根(abcde)となります。ここで、幾何平均を縦にみれば a・・・e の絶対値は分からずとも、a:b:c:d:e の比が判明します。また、各升目は各重要度の1対比ですから、10点スコアを按分した6:4などを互いに割った数字で代用できます。よって、図2の計算が成り立つ次第です。
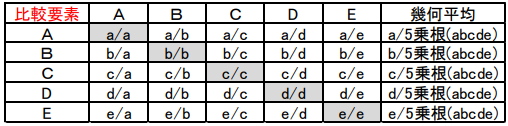
図3.重要度算出ロジック (按分スコア比)
ここで、按分スコア a:b=7.5:2.5, a:c=7.5:2.5, b:c=5:5 の事例を検討します。このスコアなら、“A がか
なり重要”との思いでしょう。
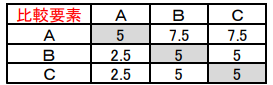
図4.按分スコア 事例
スコア比に変換する...