レオロジーを深く知る（その８）物質の三態とその由来

前回のレオロジーを深く知る（その７）物質の三態とその由来に続けて解説します。

1.4 固体と液体の違いとは

ここまでの議論で、固体のミクロなモデルの振る舞いは少しずつ理解が進んできました。次に、固体と液体との違いについて、シミュレーションも活用しながらイメージを膨らませていきましょう。

1.4.1 固体と液体の間の相転移

固体と液体との境目について考えていきましょう。具体的には、固体側から見たときには融解現象であり、液体からでは結晶化ということになります。このとき、マクロに見れば、融解や結晶化が生じるときに比熱や体積に「飛び」が生じることが知られています。この実験事実に基づいて、物質の内部で生じているミクロなスケールにおいては、内部の粒子のパッキングが変化し、さらに内部の粒子の運動状態も変化していると考えられています。

1.4.2 MD シミュレーションでの確認

この相転移現象に基づく粒子の振る舞いの変化を、分子動力学シミュレーションで見てみましょう。図 9 に示した固体のシミュレーションと同じ初期構造のものを、シミュレーション温度を高温に（T=1.0）した場合です。この動画リンクをクリックすれば、動画を見ることができます。温度の上昇により、粒子の運動が激化して安定位置から脱出しています。そして、粒子が固体状態での規則構造にとどまることなく、自由に運動していることが確認できます。固体状態の規則的な構造が乱れていますので、粒子間の距離も伸びているようですが、このスナップショットからはそこまではわかりません。

1.4.3 粒子間の状態を観る

次に、粒子同士の相互の位置関係、すなわち、並び具合を評価する方法について簡単に説明します。

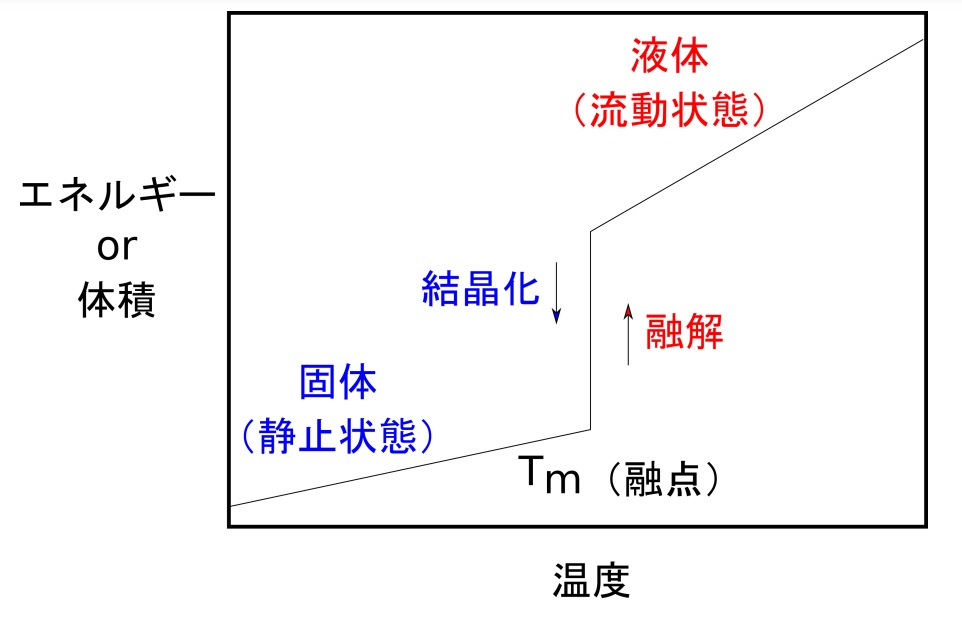
図10. 固体と液体の相転移

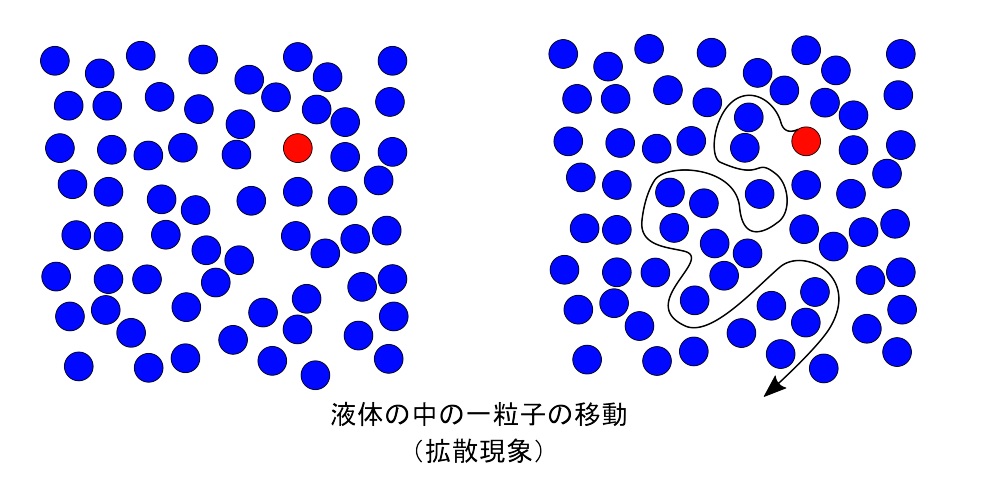
図11. 分子動力学シミュレーションで見た液体

物質が粒子から成り立っている場合「動径分布関数」という考え方に基づいて、内部の粒子の状態を評価できます。これは、以下のような手順となっていて、1 つの粒子から見た場合の他の粒子の存在比率を粒子間の距離の関数として表すことができます。^注）図 12 に動径分布関数の原理を示しました。

注）この方法はシミュレーションだけで行われているのではなく、実験においても散乱関数という X 線や中性子線を物質に照射して内部の微細な構造を測定する場合にも使われています。

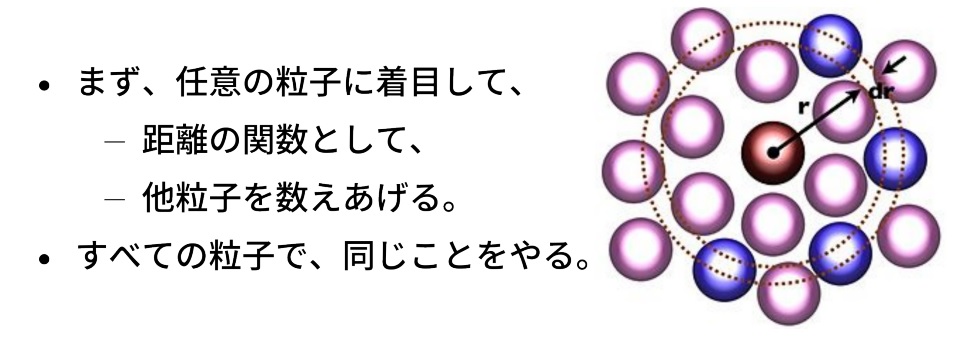
図.12 動径分布関数の原理

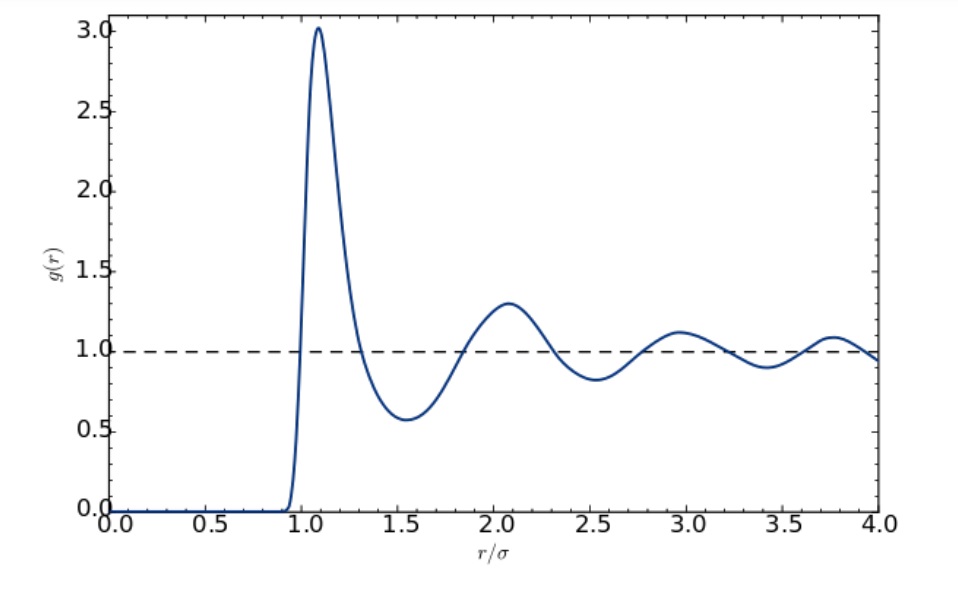
これまでに示した固体と液体のシミュレーションから求めた動径分布関数の比較を図 13 に示しました。固体の動径分布関数を考えると、液体のそれと比べて細かいピークが見られ、その最低値は 0 に近づいています。これは、特定の位置における粒子の偏在と、その間の空間に粒子が存在しないことを示しています。一方、液体の動径分布では短い距離の部分に数本のピークが見られますが、遠距離ではピークが見えなくなります。また、最低値も固体より高くなっています。この振る舞いから、液体内では粒子の相互作用がたかだか粒子数個分の比較的短距離に限定されていること。でも、全体としては不規則な配置を持っていることが推測されます。

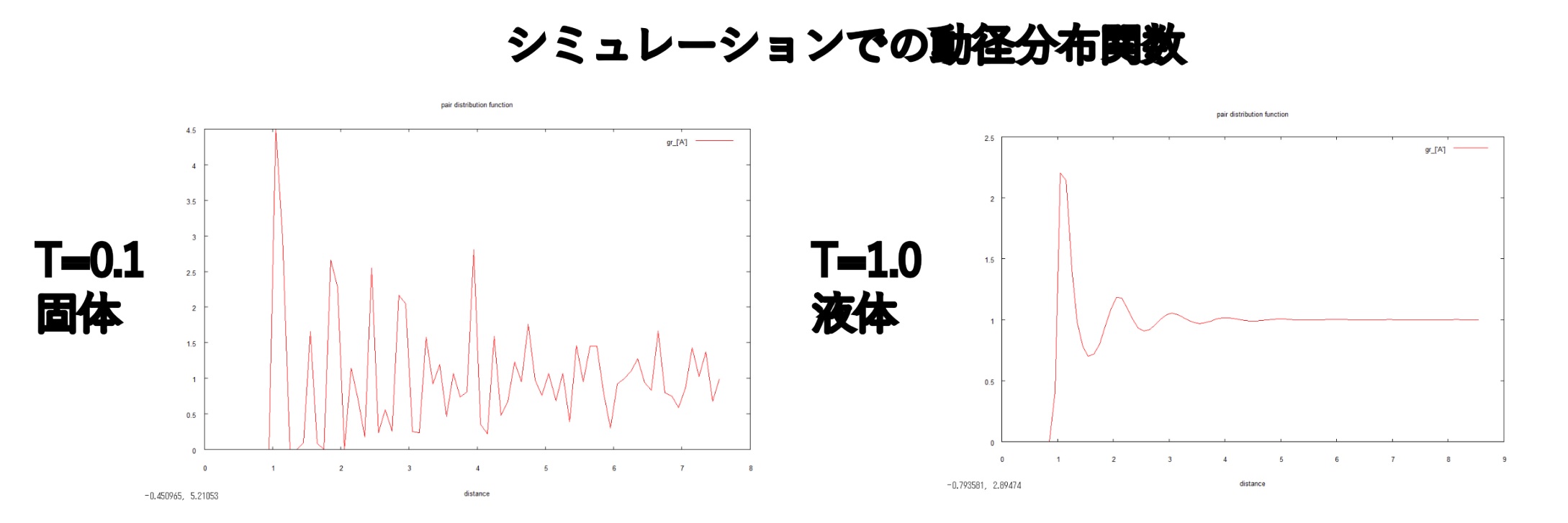
図.13 シミュレーションでの動径分布関数の比較

1.4.4 液体をミクロに観ると

さらに、液体における密度のゆらぎについて少し詳しく考えてみましょう。図 14 に液体の動径分布関数のイメージ図を示しました。液体における粒子の相互の位置は規則的ではなく、粒子径 (r/σ=1)よりも少し離れたところにピークがあり、それよりも少し遠くでは平均値より高いものと低いものが繰り返しています。これは、局所的な密度の濃淡が生じていることを表しています。シミュレーションの動画でみられたような乱雑に並んだ粒子の異なる方向への運動は、それぞれの粒子が密度の高い場所から混み合っていない場所への移動を繰り返していると捉えることができます。

ここで注意していただきたいのは、コップの中の水のように周りが拘束された状態では、水は止まって見えているということです。そのような状態においても、ミクロに見れば、粒子は絶えず移動して入れ替わっています。しかしながら、...