1．表が出やすいコインの判定と有意水準
有意差の判定を、コイントスの事例で考えてみましょう。普通のコインならば、コイントスで表裏の出る割合はほぼ同じと考えられます。実際は表裏が全く同数という事は無く、どちらかが多くなります。ではコイントスを60回行ったときに、表が何回以上出れば表が出やすいコインと言えるでしょうか？
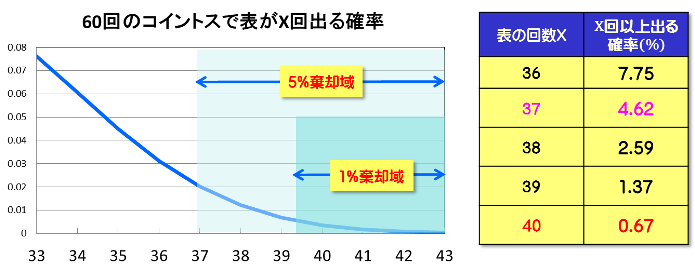
60回の試行で表が50回も出れば、間違いなく表が出やすいといえるでしょう。では37回表が出たとしたら、表が出やすいコインと言えるでしょうか？それとも偶然と言えるでしょうか？
それを統計的に判断する為には表が37回出る確率を計算し、それが一定以下の数値であれば出やすいと判断を下します。この偶然だと言わせない数値的な判定基準(確率)が、有意水準若しくは危険率と呼ばれるものです。
慣例的に有意水準は1%、5%、10%のいずれかが用いられます。 例えば有意水準5%で検定を行うとすれば、37回表の出る確率が5%以下であれば滅多に生じないケース(20回に一回程度)であり偶然とは言えない、つまり統計的に表が出やすいと判定する事になります。
図1．コイントスの判定
2．帰無仮説と対立仮説
検定では事象が偶然で生じたのか、めったに出ないイベントとして生じたのかを判定するために二つの仮説を立てます。これらを帰無仮説と対立仮説と呼びます。 このコイントスの事例で言えば、次のように帰無仮説と対立仮説を立てます。
・帰無仮説H0：表と裏の出る確率は同等
・対立仮説H1：表が裏より出やすい
表がX回出る確率が有意水準以下なら、滅多にない事が生じたとして対立仮説H1が支持され、帰無仮説H0は棄却されます。一方確率が有意水準より大きければ、H0は棄却できません。注意すべき点として、確率が有意水準より大きくても、積極的にH0が成り立つと言えるわけでは無い事です。H1(表が出やすいと)が断言出来ないだけで、H0(表も裏も確率は同等)である主張は出来ず、あくまで弱い否定に留まります。
3．有意水準による検定結果の違い
次にコインの表と裏が出る確率がそれぞれ1/2の場合に、60回コイントスを行った場合の表がX回出る確率を計算したものが図2です。
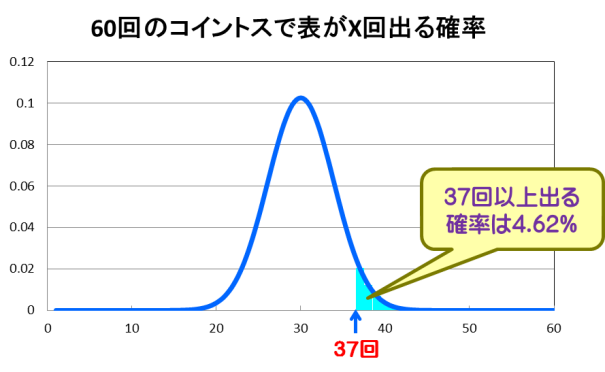
図2．コイントスを60回行った場合の表がX回出る確率
37回以上表が出る確率は4.62%であり5%以下となります。よって対立仮説が支持され帰無仮説は棄却されます。 つまりこのコインは表が出やすいと言える事になります。
この様に検定とは、仮説を立てて...
