1.正規分布とは
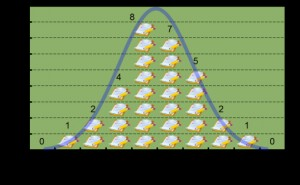
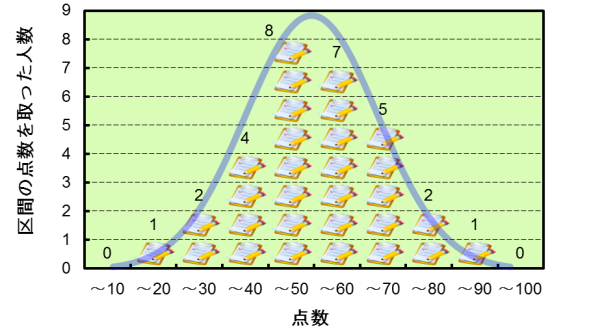
一般に自然界のデータ分布は左右対称の釣鐘形状になります。例えば平均が50点の試験があれば、そこを中心に点数の分布が左右に広がります。受験者数nが大きくなればなるほど平均値周辺の人数が増え、分布の形は滑らかになり正規分布という形に近づきます。
正規分布は最も基本となる分布の一つで、自然界の分布は多くがこの分布の形を取ります。正規分布は、ばらつきが大きければすそ野の広い富士山形状となり、小さければシャープな釣鐘型形状となります。
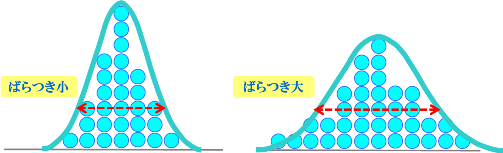
分布が下図の左の様であればばらつきが小さいことを示し、試験は受験者による差が少なく実力が拮抗していたと言えます。逆に右の様に幅が広ければばらつきが大きい、つまり点数が良かった人も悪かった人もいたことを示します。
2.正規分布と標準偏差の関係
別項で、ばらつきを示す統計量として標準偏差σについて述べました。 シャープな正規分布は、σが小さい分布です。ブロードな正規分布はσが大きい分布です。
では正規分布の中央から±1σの範囲に入るのは全体の何%でしょう?先ほどの試験結果の例で考えてみましょう。平均50点で標準偏差が10点だとすると±1σの範囲は40点から60点の範囲に当たります。 同様に±2σは30~70点、±3σは20-80点の範囲に該当します。この時の分布は次の図のようになります。
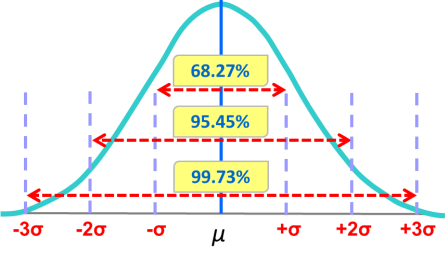
即ち各得点の範囲に入る受験生は次の割合です。
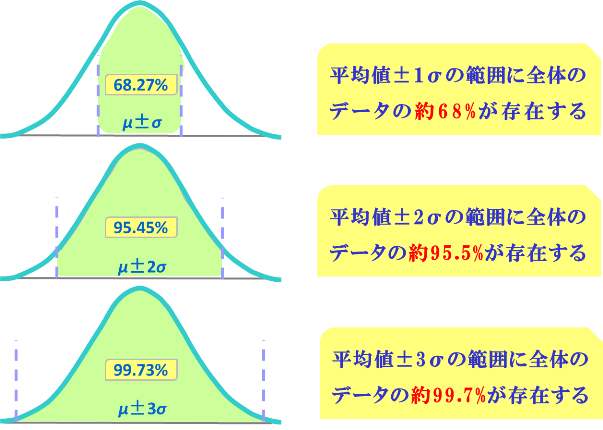
•±1σ (40-60点):約68%
•±2σ (30-70点):約95%
•±3σ (20-80点):約99.7%
良く使う偏差値は、平均と標準偏差を元に計算します。偏差値は、平均点を取れば点数の大小に関わらず50となるような数値です。
次にこの正規分布を、規格の中心が100mmの部品の寸法分布で再度考えてみます。理想は、すべての部品が100mmピッタリになる事です。しかしこれまで述べてきたように、残念ながら必ずばらつきが生じます。もし規格幅が100mm±1mmであれば98.5mmや101.5mmの部品は納品できません。平均が100mmで標準偏差が0.3mmだとしたら、100±0.9mmの範囲に99.7%が入ります。逆に言えば1000本作成した中に、規格外れが3個ほど発生する可能性があります。もし1日10万個を作る大量生産部品ならば300個の不適合品が出来る事になります。
規格幅99.0~101.0mmの中に分布がすっぽりと収まるのが理想です。合格率を高めて不適合を減ら...