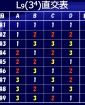
直交表とは、与えらえた複数因子の全水準を組み合わせなくても、各因子の効果が独立して評価できる組み合わせの表で、英語ではOrthogonal TableやOrthogonal Arrayといいます。一昔前とは異なり昨今の工業製品は複雑化しており、特性値の仕様を満足させるのに2つや3つの因子を取り上げただけでは実現不可能になっています。高度な製品の特性には数百個の因子が影響していると考えて良いでしょう。
一方世の中はますます短い開発/設計期間を要求してきており、実験にあたっては出来るだけ多くの因子を出来るだけ少ないサンプル数で評価するという矛盾した項目が要求されます。因子数が多い場合に通常の多元配置実験を実行すると、原理的には気が遠くなるようなサンプル数を作ることになって現実的ではありません。
そんな時に「直交表」を使うと効率的です。直交表を用いた実験計画は主に日本で発展した方法で、日本の工業製品の優秀さの一つの理由であると言われるくらい優れたツールです。
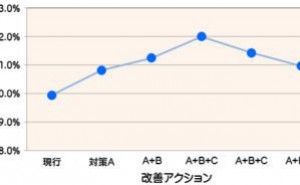
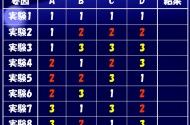
下の表1は7つの因子A~Gに対して2水準の差を評価するときに良く使われる水準組合せで「逐次実験」と言われます。全ての因子を第1水準に取った実験(サンプル)1に対して、実験2~8で一つずつ因子の水準を振り、因子の効果を見ます。
| 要因 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 実験1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 実験2 | 2 | 1 | 1 | 1 | 1 | 1 | 1 |